The medium-energy concentrator spectrometer on board
the BeppoSAX X-ray astronomy satellite
G. Boella1,3, L. Chiappetti1,
G. Conti1, G. Cusumano2,
S. Del Sordo2, G. La Rosa2, M.C. Maccarone2,
T. Mineo2, S. Molendi1, S. Re2,
B. Sacco2, and M. Tripiciano2
- 1 CNR - Istituto di Fisica Cosmica e Tecnologie Relative, Via Bassini 15, 20133 Milano, Italy
- 2 CNR - Istituto di Fisica Cosmica ed Applicazioni
dell'Informatica, Via Ugo La Malfa 153, 90146 Palermo, Italy
- 3 Dip. Fisica, Università di Milano, Via Celoria 16,
20133 Milano, Italy
Abstract
The scientific instrumentation on board the
X-ray Astronomy Satellite BeppoSAX includes a Medium
Energy Concentrator Spectrometer (MECS), operating in
the energy range 1.3 - 10 keV, which consists of three units,
each composed of a grazing incidence Mirror Unit and of a position
sensitive Gas Scintillation Proportional Counter. The design and
performance of the MECS instrument are here described, together
with its on-ground calibration.
Key words: Instrumentation: detectors - X-rays: general
Introduction
The X-ray Astronomy Satellite BeppoSAX is a joint project
of the Italian Space Agency (ASI) and the Netherlands Agency for Aerospace
Programs (NIVR) devloped by a consortuim of institutes in Italy and
The Netherlands, including the Space
Science Department of ESA (SSD).
BeppoSAX, with an expected lifetime of up 4 years, is devoted
to systematic, integrated, and comprehensive studies of
galactic and extra-galactic sources in the wide energy
band 0.1 - 300 keV. The spacecraft, three axis stabilised
and with a total mass of ~400 Kg, has bee launched by an
Atlas G-Centaur on April 30, 1996, 04:31 GMT, into a circular
equatorial orbit of
~3oinclination and 600
Km altitude. The scientific payload comprises four Narrow
Field Instruments NFI (Low Energy Concentrator Spectrometer
LECS, Medium Energy Concentrator Spectrometer MECS, High Pressure
Gas Scintillation Proportional
Counter HPGSPC, Phoswich Detection System PDS) all
pointing in the same direction, and two Wide Field Cameras WFC,
pointing in diametrically opposed directions
Send offprint requests to:
M.C. Maccarone: cettina@ifcai.pa.cnr.it
perpendicular to the NFI common axis. A detailed description of
the entire BeppoSAX mission can be found in
Butler & Scarsi (1990) and in Boella et al. (1996).
The MECS, operating in the medium X-ray energy
band, is one of the NFI instruments onboard BeppoSAX.
The main scientific objectives of the MECS are: spectroscopy
from 1.3 to 10 keV (E / (D EFWHM) in the range
6 - 16); imaging with angular resolution at the at the
arcmin level; timing variabilty on time scales down to the millisecond.
In this paper we give a description of the MECS instrument and
its performance. Design, development, calibration and data
analysis have been carried out by the
MECS team at the IFCAI-Palermo and IFCTR-Milano
Institutes in Italy, supported by the Italian Space Agency
ASI in the framework of the BeppoSAX mission. The
MECS on-ground calibration was performed at the X-ray
PANTER facility of the Max Planck Institute, Germany;
preliminary results of on-ground calibration analysis can
be found in Boella et al. (1995) and in Molendi et al.
(1995).
2. MECS description
The MECS consists of three units, each composed of a
grazing incidence Mirror Unit (MU), and of a position
sensitive Gas Scintillation Proportional Counter (GSPC)
located at the focal plane. The MUs are connected to the
GSPCs by a Carbon fiber envelop, about 2 m long. MECS
overall performance is listed in Table 1. The quoted angular
resolution values indicate the radii encircling 50% and
80% of the total signal, respectively (r50, r80).
2.1. Mirror unit
Each MU is composed of 30 nested coaxial and confocal mirrors.
The mirrors have a double cone geometry to
approximate the Wolter I configuration (Citterio et al.,
1985), with diameters ranging from 68 to 162 mm, total
Table 1. MECS overall performance
Parameter | Value
|
| |
|
| Field of View | 28' radius
| |
| Focal length | 1.85 m
| |
| Angular resolution: |
| |
| '' at 1.5 keV | r50=105" , r80=165"
| |
| '' at 6.4 keV | r50=75" , r80=150"
| |
| '' at 8.1 keV | r50=75" , r80=150"
| |
| Energy range | 1.3 - 10 keV
| |
| Energy resolution | ~8 (6/EkeV)½ % FWHM
| |
| Total on-axis effective area: |
| |
| '' at 1.5 keV | 31 cm2
| |
| '' at 6.4 keV | 150 cm2
| |
| '' at 8.1 keV | 101 cm2
| |
| Time resolution | 15 micro sec
| |
| Image binning | 256x256 pixels
| |
| Image pixel dimension | 20" by 20" square
| |
| Energy binning | 256 channels
| |
| Burst length binning | 256 channels
| |
| Total maximum throughput | 2000 cts/sec (4 Crab)
|
length of 300 mm, thickness from 0.2 to 0.4 mm and focal
length of 1850 mm. The MU design was optimized to have
the best response at 6 keV. A replica technique by nickel
electroforming from super-polished mandrels was used to
build up the mirrors (Citterio et al., 1988). A 1000 Å thick
gold layer provides the X-ray reflecting surface. The 30
mirrors are nested using two front-end spiders with eight
arms. The geometrical collecting area of each MU is 123.9
cm2 ; the spiders and an active anti-ions grid reduce this
geometrical area by about 18%. The measured radius for
50%, 80% and 90% encircled energy are of the order of
40, 110, and 210 arcsec at 8 keV, respectively. A more
detailed description of the MU Point Spread Function can
be found in Conti et al. (1993, 1994).
2.2. Detector unit
The focal plane detectors are Xenon filled GSPC,
working in the range 1.3 -10 keV with an energy resolution
of ~8% at 5.9 keV and a position resolution of ~0.5 mm
(corresponding to 1 arcmin, aproximately) at the same energy.
The gas cell is composed by a cylindrical ceramic body
(96 mm internal diameter) closed, at the top, by a
50 -6m thick entrance Beryllium window with 30 mm
diameter and, on the bottom, by an UV exit window made
of Suprasil quartz with 80 mm diameter and 5 mm thickness,
as schematically shown in Fig. 1. In flight, the getter
can be activated to purify the gas, if necessary.
The entrance window is externally supported by a
Beryllium strongback structure, 0.55 mm thick, consisting
of a ring (10 mm inner diameter, 1 mm width) connected
to the window border by four ribs, as shown in Fig. 2.
 Fig. 1. Schematic view of the MECS instrument: gas cell and
position sensitive GSPC
Fig. 1. Schematic view of the MECS instrument: gas cell and
position sensitive GSPC
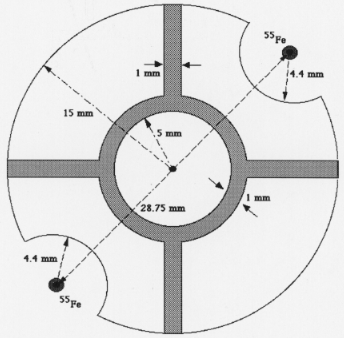 Fig. 2. Geometry of the strongback
Fig. 2. Geometry of the strongback
An X-ray photon absorbed in the gas cell liberates a
cloud of electrons. A uniform electrical field across the
cell drifts the cloud up to the scintillation region, with an
higher electric field, where UV light is produced through
the interaction of the accelerated electrons with the Xe
ions. The amplitude of the UV signal, detected by a PMT,
is proportional to the energy of the incident X-ray. The
duration of the signal, the so-called Burst Length (BL),
depends on the interaction point and it is used to discriminate
genuine X-rays against induced background events.
BL rejection may be carried out on board and/or onground. The
BL rejection mechanism on board is based
on a programmable BL acceptance window (not energy
dependent). Two grids inside the cell separate the absorption/drift
region (20 mm depth) from the scintillation region (17.5 mm depth).
The UV readout system consists of
a crossed-wire anode position sensitive Hamamatsu photomultiplier
(PMT) with quantum efficiency of ~20%. The
high voltage nominal values are -8 kV for the Be window,
-7 kV for the scintillation grid, 1000, 992, and 943 V for
the PMT of ME1, ME2, and ME3 units, respectively.
Two 55Fe collimated calibration sources (nuclear line
at 5.95 keV), with an emission rate of ~1 count per second,
are located, diametrically opposed, near the edge of the
Be window. These inner calibration sources, continuosly
visible at the edge of the Field of View (FOV), allow the
monitoring of the detector gain. Furthermore a passive ion
shield is placed in front of the detector. The focal plane
detector characteristics are shown in Table 2.
Table 2. Focal plane detector
| Parameter | Value
|
|---|
| |
|
| Position resolution | 0.7 (6/E)½ arcmin
|
| Gas Type | Xenon
|
| Gas filling pressure | 1.0 atm at 25oC
|
| X-ray window: |
|
| '' material | Beryllium
|
| '' diameter | 30.0 mm
|
| '' thickness | 50-6m
|
| '' central region diameter | 10 mm
|
| '' support frame: |
|
| '' '' material | Beryllium
|
| '' '' thickness | 0.55 mm
|
2.3. Electronic unit
The MECS electronic processing takes place, almost entirely,
in the Electronic Unit; only signal buffering is performed
near the PMTs (one for each detector).
From each PMT, six signals are transferred to the Electronic
Unit: Trigger, Energy, X 1, X 2,
Y 11, and Y 22. All
the
signals are converted from current to voltage before to be
passed to the Electronic Unit; in particular, the Energy
and the position signals are integrated with a little time
constant (few hundred of nanoseconds). The Trigger signal is
taken from the 14thdynode whereas the Energy is
taken from the 15thdynode (the last one). The X1 and
X2 signals come out from the 16 anode wires (connected
through a resistor divider) that give information about the
X position. The same is valid for Y1 and Y2.
In the Electronic Unit there are three analog processing
modules (one for each detector) followed by one Event
Processor that arranges the data in packets sending them
to the Communication Processor.
All the signals incoming from a single PMT (Trigger
excepted) undergo to a baseline restoring and then they
are integrated by Gated Integrators with fixed
25-6s integration time. The X and Y positions
are calculated (via hardware) from the original X1, X2, Y1
and Y2 in accordance to the formulas:
X = [X1 - X2] / [X1 + X2]
Y = [Y1 - Y2] / [Y1 + Y2]
The Burst length BL signal is obtained from the Energy through a
constant fraction, zero crossing and Time-to-amplitude Converter chain.
There is a programmable selection logic, working on Energy and
BL signals, to reject events before the A/D
conversion. If during the integration time two trigger
pulses are recognised, then the Pile-up Logic will reset
the electronics in order to be ready for the next event.
An Event Qualification Logic increments the Ratemeter
registers, that are read at 1 s rate.
After the A/D conversion the data are saved into a
FIFO register together with the event time. Data from
the FIFO are read by the Event Processor and submitted
to a rejection rule with programmable windows for Energy,
BL, X and Y. Finally data are packed and written
in a Dual Port RAM from where they will be read by the
Communication Processor.
3. On-ground calibration set-up
The three flight MECS units have been extensively calibrated
(~170 millions photons per unit) at the 130-meter
long X-ray PANTER facility of the Max-Planck-Institut
für Extraterrestrische Physik in Munich, during a period
of 7 weeks in October-November 1994. The limited size
of the PANTER beam did not allow a simultaneous calibration of
all units; therefore two MECS units, hereafter
named ME2 and ME3, were calibrated together during
the first run of measurements while the third MECS unit,
hereafter named ME1, was calibrated during the second
run together with the LECS instrument (Parmar et al., 1996).
A detailed description of the experimental set-up used
for on-ground calibrations can be found in Boella et al.
(1995). Briefly, the MUs and the detectors were mounted
on two separate optical benches, remotely controlled by
manipulators (one linear and two rotational for the MUs,
and three linear for the detectors); moreover, the assembly
MUs-detectors was mounted on a table that could be rotated
and tilted for off-axis measurements. In particular,
the linear manipulator of the MUs bench could position,
in front of the detectors, alternatively the two MUs, or
two 40 mm diameter holes for direct beam measurements
(the so-called flat fields), or two multipinhole masks with
a square matrix of 123 holes (0.561±0.007 mm diameter)
with 4 mm pitch. The MUs and detectors alignment was
performed in two steps: a first rough alignment with a
divergent He-Ne laser beam that simulates the X-ray PANTER
beam, and a final adjustment at 1.5 keV by using
those photons that, as a result of the divergence of the
beam, are reflected only by the first cone of the MUs.
Two interchangeable X-ray sources are available at the
PANTER facility: the first one is directly installed in
vacuum for energy lines up to 3 keV; the second one, separated
from the vacuum by a Be window, is used for higher
energies. Both systems are equipped with a set of filters of
various material and thickness. The high voltage supply,
the emission current of the X-ray source, and the position
of the filter wheel can be adjusted to cut the source continuum
bremsstrahlung and to obtain the desired counting
rate and the more convenient energy spectrum. An independent
proportional counter (Monitor Counter) is placed
at the entrance of the test chamber and it is used to
monitor the X-ray beam intensity. All the information concerning
the basic experimental conditions (time, X-ray source
voltage and current, manipulator encoder outputs, monitor
counter rate) was continuously stored in housekeeping
files useful for the off-line calibration data analysis.
The instrument Electronic Unit, common to all the
three MECS units, was connected to a Test Equipment
including a bus probe emulating the satellite OnBoard
Data Handling bus. Test Equipment control, instrument
control, and data acquisition (in the form of block transfer
bus data packets) were performed via a VAX-station
connected on a Local Area Network with a second VAXstation
for intermediate storage, with two PCs for Quick
Look, and with one more PC for data archiving onto
magneto-optical disks for off-line analysis. The instrument
Electronic Unit performed very well and supported source
rates up to 4000 cts/s beyond the specification of 2000
cts/s.
The principal X-ray energy lines used to calibrate the
MECS units are reported in Table 3. For almost all the energy
lines, three main kind of measures were performed:
mirror units (MU) on-axis and off-axis, flat fields (FF) of
the detectors alone, and multipinhole scans of the detector
units alone. All these measurements were performed
at the nominal instrument setting. The statistical quality
of the data was very high: a typical MU acquisition contained
about half a million events. Additional measurements of the
detector performance were performed changing the high
voltage of the cell and of the PMT respect
to their nominal values; moreover, the behaviour of the
detector has been checked in function of the count rate.
4. Instrument performance
In the following the main results of the on-ground calibration
analysis are presented, together with the overall
MECS performance.
Table 3. PANTER calibration lines (a) ME1 only;b) ME2 and ME3 only)
|
Line | Energy | Line | Energy
|
|---|
| | (keV) | | (keV)
|
|---|
| Cu Lalpha | 0.93a) | Ag Lalpha | 2.99
|
| Mg Kalpha | 1.25b) | Ti Kalpha | 4.52
|
| Al Kalpha | 1.49 | Cr Kalpha | 5.42
|
| Si Kalpha | 1.74 | Fe Kalpha | 6.41
|
| P Kalpha | 2.01 | Cu Kalpha | 8.06
|
4.1. Temperature gain dependence
The lack of a temperature readout from the Test Equipment
did not allow us to investigate the gain dependence
on temperature during the MECS calibration at the PANTER
facility. However, during the integrated satellite tests
in ESTEC in October/November 1995, we were able to
collect useful data for the ME1 and ME3 units. A preliminary
analysis of these data indicates that the gain is anticorrelated
with the temperature, and that variations of
1o C produce variations of ~1.5% in the gain.
A more accurate measurement of this dependence will be performed
during the in-flight Science Calibration and Verification
(SVP) Phase.
4.2. Position gain dependence
A dependence of the gain on the position is present in
all three detectors (in the sense that a photon falling at
the edge of the detector will be revealed in a different
PHA channel than a photon falling close to the center);
this dependence can be calibrated by analysing individual
spectra of each spot of the multipinhole measurements.
The core of the line in each spectrum has been fitted with
a gaussian, and the peak position in channels has been
associated to the spot position in pixels, obtaining a sparse
set of values Gi = G(xi,yi). For each data acquisition,
a gain map has been derived with a bi-quadratic interpolation of
the above values on each pixel within the detector window. The
values have been normalized to the
gain at the detector center, obtaining a relative gain map
g(x,y) = G(x,y) / G(xo,yo). The relative gain has been
found to be extremely stable with energy, as well as unaffected
by time variations of the absolute gain (this is
not surprising as the spatial dependence of gain is due to
geometrical disuniformities in the PMT anodes and/or in
the Suprasil quartz window); therefore, the gain maps of
all the multipinhole measurements at all energies can be
averaged to produce a single high accuracy gain map per
detector unit.
The relative gain maps are shown in Fig. 3 for the
three ME1, ME2, and ME3 units, respectively. The range
of the relative gain (assuming 1.00 in the detector centre)
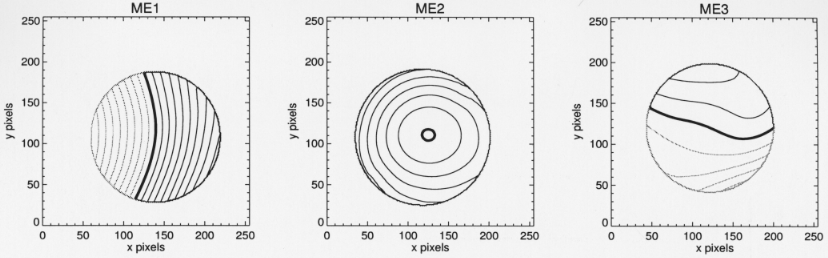 Fig. 3. Relative gain maps (gain as percentage of the value
at detector centre). Thick lines indicate a gain of 1.00. Contours
are spaced by 0.01. Contours lower than 1.00 are in lighter shade
Fig. 3. Relative gain maps (gain as percentage of the value
at detector centre). Thick lines indicate a gain of 1.00. Contours
are spaced by 0.01. Contours lower than 1.00 are in lighter shade
is 0.90 - 1.10 for ME1, 0.99 - 1.06 for ME2 and 0.96 - 1.03
for ME3, with a rms error 0.002 on almost all the field of view
(excluding the 56Fe calibration sources region where
data were extrapolated).
4.3. Energy to channel conversion
Energy-to-channel conversion, energy resolution, and
spectral profile of the MECS instrument have been determined
from a detailed analysis of the calibration spectra.
For each PANTER calibration line (see Table 3), on-axis
and off-axis MU measurements have been analysed.
Energy spectra have been accumulated by selecting
data in Burst Length in order to reject both double events
(long BL) and events that convert in the scintillation region
(short BL), as will be explained in Sect. 4.7.4. The
relative gain maps (see Fig. 3) have been used to correct
for the position gain dependence. Temporal gain dependence,
mainly due to the temperature, have been taken
into account by using the mean gain of the two 55 Fe inner
calibration sources.
Fig. 4 shows the Cr line spectrum as detected by the
ME2 unit as an example. Apart from the main peak, the
spectrum shows several characteristics. In the low energy
part are clearly present some features produced by the escape of
fluorescence photons from the detector gas cell;
they are present only for incident energies greater than
4.78 keV (the Xe L-edge). The phenomenon strictly depends on the
geometry of the cell and on the gas filling
pressure. In the case of the MECS, fluorescence photons
mainly escape from the Be window and the escape fraction
is expected to decrease when the energy increases, due to
the greater penetration depth of the incident photon.
The bridge connecting escape and main peaks is due to
the loss of a part of primary electrons for window attachment. In
fact, in consequence of the primary interaction
of the X-ray photon with the Xe atoms, an electron cloud
is produced. This cloud diffuses toward the scintillation
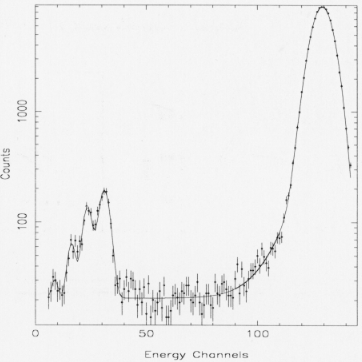 Fig. 4. Energy spectrum of the Cr line (5.42 keV) with the
fitting curve superimposed
Fig. 4. Energy spectrum of the Cr line (5.42 keV) with the
fitting curve superimposed
region under the effect of the drift electric field. However,
if the primary interaction takes place near the Be window, part of electrons is captured by the window itself,
producing a smaller energy deposit (Inoue et al., 1978).
The spectra are fitted as a whole (see as example the
continuous line in Fig. 4) by a function which is a sum
of various components: a gaussian for the main peak, four
gaussian for the escape peaks, and an exponential plus a
constant to model the electron attachment phenomenon.
For energies below 4.78 keV, the fitting model is simplified
due to the absence of the escape peaks.
In some cases, as for the Ti spectrum shown in Fig. 5,
there is clear evidence of a secondary, unresolved peak, the
two components being the Kalpha and Kbeta Ti lines; a better fit
is then obtained by using two gaussian curves (the dotted
curve in Fig. 5 represents the fit with a single gaussian,
only).
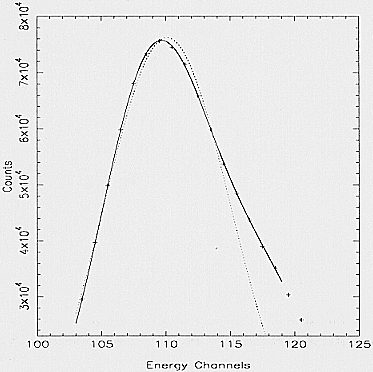 Fig. 5. Energy spectrum of the Ti line (4.52 keV) of the central
peak region. The dotted line refers to a single gaussian fit; the
continuous line represents the double gaussian fit
Fig. 5. Energy spectrum of the Ti line (4.52 keV) of the central
peak region. The dotted line refers to a single gaussian fit; the
continuous line represents the double gaussian fit
In Table 4 the total escape fractions are reported. The
experimental values are in good agreement with the prediction of a numerical model of the detector; no variation
has been found as function of the incident photon position.
Table 4. Experimental total escape fraction
|
Line | Energy | Escape
|
|---|
| | (keV) | (%)
|
| Cr | 5.42 | 2.23
|
| Fe | 6.41 | 1.84
|
| Cu | 8.06 | 1.42
|
Fig. 6 shows the results of the gain analysis for the
detector unit ME2 (ME1 and ME3 units present a similar
behaviour). The discontinuity at 4.78 keV (the jump in
the detector gain) is caused by a decrease in the photonelectron conversion efficiency of the gas at the Xe L-edge
(Santos et al., 1991, Dos Santos et al., 1993). This effect
was also found in the EXOSAT, Tenma (White, 1985), and
Spacelab GSPC detectors. The solid straight line in Fig. 6
corresponds to the best fit of the experimental points on
each side of the edge (Mg, Al, Si, P, Ag and Ti lines for
the left side; Cr, Fe and Cu lines for the right side).
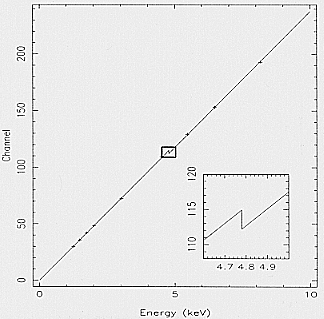 Fig. 6. Gain vs. energy relationship for the ME2 detector unit.
The discontinuity region due to the L-jump is zoomed in the
insert
Fig. 6. Gain vs. energy relationship for the ME2 detector unit.
The discontinuity region due to the L-jump is zoomed in the
insert
The fit procedure performed with the law
| Gain = | A · E + B1 | for E 4:78 keV
|
A · E + B2 | for E 4:78 keV
|
with Gain expressed in channel and E expressed in keV,
gives the best A, B1 and B2 coefficients for each detector
unit; the derived value of the L-jump discontinuity, averaged over the three units, is 110±15 eV, in good agreement
with previous measurements (Lamb et al., 1987, Dos Santos et al., 1993).
4.4. Energy resolution
The spectral analysis allows to derive the energy resolution
of the three MECS units for each PANTER calibration line.
The experimental values, in the form of Full Width
Half-Maximum (FWHM), have been fitted by:
[(D E) / E] = A (6 / E)½ (%)
where E is expressed in keV. The best fit values for the
parameter A are 8.30(±0.08), 8.10(±0.08) and 7.68(±0.07)
for ME1, ME2 and ME3 respectively, in agreement with
the expectation for this kind of detector. In fact, the
theoretical limit for the energy resolution of a GSPC is:
[D E / E] (% FWHM) = 2:35 (F / N)½ x 100
where F is the Fano factor and N is the mean number of
primary electrons produced by the X-ray photon. For the
Xenon, typical value of the Fano factor is ~0.2. The mean
energy to produce an electron-ion pair in Xenon is 22 eV.
Using these values, the theoretical limit for the energy
resolution is ~6.50% at 6 keV (Ramsey et al.,1994).
In the central region of the detector gas cell (10 mm
radius) no position dependence of the energy resolution is
pointed out within the experimental errors.
As an example, the ME1 spectral resolution versus energy is plotted in Fig. 7.
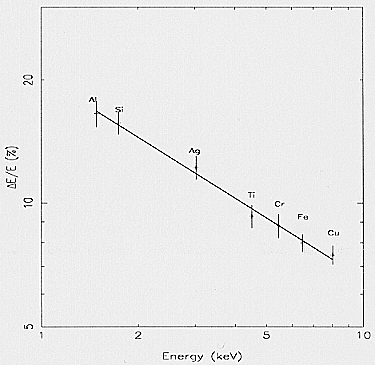 Fig. 7. Spectral resolution vs. energy relationship for the ME1
detector unit
Fig. 7. Spectral resolution vs. energy relationship for the ME1
detector unit
4.5. Image linearization
The position response of the detector is affected by some
nonlinearities coming from three main contributions. The
first most likely derives from spatial disuniformities in the
PMT gain; the second one is due to a geometrical effect,
i.e. different scintillation positions are seen by the PMT
under different solid angles, leading to a variation in the
light collection and then to an erroneous determination of
the scintillation event position. These two effects are energy independent. The third contribution may be related
to the distortion of the electric field near the Be window,
due to a slight curvature of the window itself. This effect is
more enhanced at low energy because of the shorter mean
penetration depth of low energy photons (0.4 mm being
the mean penetration depth of 1.5 keV photons with 1 atm
of Xe) that produce a shift of the scintillation point with
respect to the point in which the X-ray photo-absorption
occurs.
In order to correct for these effects, the multipinhole
measurements have been analysed; for each energy at least
one measurement has been made and, in some cases, a scan
has been performed, shifting the mask by steps usually of
1 mm or (sub)multiple, in order to have a fine coverage of
the detector sensitive area with a grid of 1x1 mm. As a
preliminary step, the detector electronic axes were verified
to be aligned with the detector geometrical axes (determined by the strongback ribs) by using FF measurements
at low energies, where the shadow produced by the window strongback is clearly visible. This allowed to correct
for a slight rotation (£1o ) between multipinhole mask and
detector axes.
The barycentres (in pixels) of the spot images generated by the multipinhole mask, placed 1690 mm away
from the detector, have been calculated through a bidimensional gaussian fit. Then, taking into account the real
pitch of the holes as projected onto the Be window, a
transformation law has been derived to convert the coordinates from pixels to millimetres. The transformation law
that best fits the data is a third order polynomial, with a
dependence on the energy only in the linear term.
X = A3 [(1+ A5) / E][Kx - A1]
+ A7[Kx - A1]2 + A9[Kx - A1]3
Y = A4 [(1+ A6) / E][Ky - A2]
+ A8[Ky - A2]2 + A10[Ky - A2]3
where Kx and Ky are the coordinates in pixels,
E is the energy in keV, X and Y are the new coordinates
(expressed in mm) and Ai are the best fit parameters.
The plate scale of three dectors is ~0.17 mm/pixel.
A small anisotropy in the linear coefficients A 3
and A 4 is present between the coordinate axes: in particular,
it is ~5% for ME1, while it is negligible ( 1%)
for ME2 and ME3. Fig. 8 shows the result of the application of
the above linearization formula on the Cu line
data acquired with the multipinhole mask scan.
The transformation law reported here reconstructs the
position of the holes with a rms error of 90 -6m in a central
region of 6 mm radius, and of 120 -6m in the whole detector.
These two values should be considered upper limits
with respect to the actual values because they contain also
the contribution of the mask hole position uncertainties.
In the linearization procedure, the energy value E will be
derived from the channel-to-energy conversion law. Due
to the good MECS spectral resolution, this procedure will
introduce a small additional uncertainty of ~10 -6m. A
different approach, that is a correction of the geometrical
distortions based on a XY plane correction map, is under
evaluation.
4.6. Point spread function
The Point Spread Function (PSF) of the MECS is the
convolution of the MU PSF and the detector PSF. The
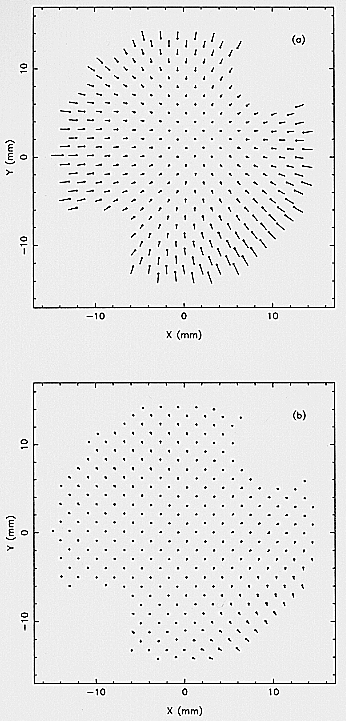 Fig. 8. Multipinhole data of the Cu line for the ME3 detector
unit. The position (0,0) refers to the center of the detector.
Each pin connects the actual hole (point of the pin) with the
measured position (pin's head). a) analysis made with
a constant plate scale factor (0.17 mm/pixels); b) analysis performed
by using the third order linearization polynomial
Fig. 8. Multipinhole data of the Cu line for the ME3 detector
unit. The position (0,0) refers to the center of the detector.
Each pin connects the actual hole (point of the pin) with the
measured position (pin's head). a) analysis made with
a constant plate scale factor (0.17 mm/pixels); b) analysis performed
by using the third order linearization polynomial
precision with which an X-ray event is localized in the
detector is essentially determined by the number of electrons
which are liberated by the interaction of the photon with
the Xenon gas contained in the detector cell. Thus the detector
PSF is expected to be a gaussian with oe / E =2 .
The multipinhole data acquisitions have been used to
measure the detector PSF. We find the data to be in good
agreement with theoretical predictions for energies E4
keV while, for E4 keV, the oe appears to be larger than
expected. The disagreement between data and model is
due to the fact that, at high energies, the size of the
PSF becomes comparable to the size of the holes, making the
pinhole approximation as a point-like source no
longer valid. In principle, the oe of the detector PSF, at
high energies, could be recovered by convolving the emission
from a hole of finite size with a gaussian, and then
by fitting this convolution to the experimental data. In
practice, it can be more conveniently derived from the FF
data, by measuring the radial distribution of photons in
proximity of the detector unit edge (a preliminary analysis
confirms the E
PSF. An analysis of the off-axis PSF is currently
under way, and it will be reported elsewhere. Preliminary
results indicate that, for off-axis angles 10 arcmin, the
departure of PSF shape from radial symmetry is relatively
small, thus allowing us to apply the radial description of
the on-axis PSF hereafter outlined. For off-axis angles 10
arcmin, i.e. outside the strongback region, an azimuthal
dependence of the PSF becomes apparent.
In order to obtain corrected on-axis PSF images of the
MECS system we have:
- accumulated images from the MU on-axis and FF data
acquisitions at each of the PANTER calibration lines
(as listed in Table 3, but the Cu Lalpha line);
- corrected the images for the spatial dependence of the
gain (cfr. Sect. 4.2);
- converted the images from raw pixels to linearized pixels (cfr. Sect. 4.5);
- applied BL and energy selections in order to reject contaminating background events;
- divided each PSF image by the FF image taken at the
same energy.
Finally we have accumulated radial profiles from the corrected PSF images.
The fit of the radial profiles have been performed with
a PSF model which is the sum of two components: a gaussian, G(r),
and a generalized lorentzian, L(r):
G(r) = cg exp[(-r2) / (2 s2)]
L(r) = cl[1 + (r / rl)2]-m
where r is the distance from the peak of the emmission and
cg, cl, s, rl, and m are the
parameters of the model. As
an example, in Fig. 9 the fit to Al line data is shown. As
can be seen, the very high statistics (~500.000 events in
each MU on-axis data acquisition) allows us to measure
the PSF up to 20 arcmin corresponding to 60 pixels.
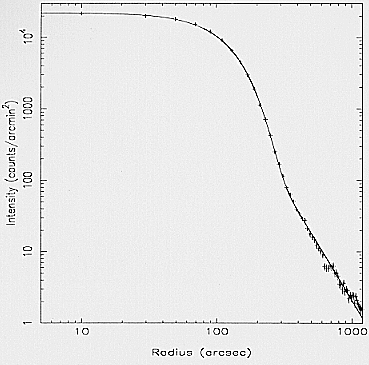 Fig. 9. Differential PSF at 1.49 keV (Al line) for the ME3
detector unit
Fig. 9. Differential PSF at 1.49 keV (Al line) for the ME3
detector unit
By imposing that the integral of the PSF over the
entire plane be equal to unity,
2 p ò PSF(r)r dr = 1
we have reduced the number of independent parameters
to four: s, rl, m,
and R, where R = (cg / cl) . The dependence
of these four parameters on energy has been reproduced
through simple algebraic functions. As an example, the fit
of the values derived at the PANTER calibration lines for
the parameter R is shown in Fig. 10.
The complete analytical expression for the on-axis PSF is:
|
PSF(r,E) = 1 / 2p[R(E)s2(E) + (r2l(E)) / 2(m(E) -1)] x
|
|
{ R(E) exp( + [ 1 + ( r / (rl(E)) )
2 ]-m(E)
|
where R(E), s(E), rl, and m(E) are algebraic functions of E.
Since both G(r) and L(r) can be analytically integrated in r dr, the PSF equation can be used to derive
a mathematical expression for the Integral Point Spread
Function:
IPSF(
r) = 2p ò PSF(r) r dr
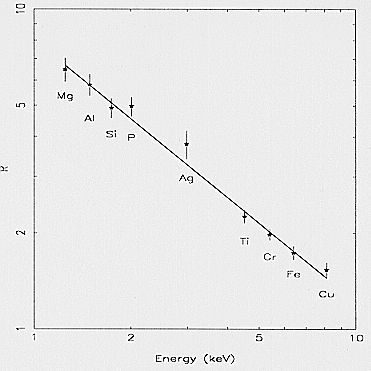 Fig. 10. The R parameter, defined as cg =c l , as a function of
energy for the ME3 detector unit
Fig. 10. The R parameter, defined as cg =c l , as a function of
energy for the ME3 detector unit
This equation has been used to evaluate the 50% and
80% Power Radius (PR) at three different energies for
the ME3 unit; the derived values are reported in Table 1
(ME1 and ME2 units give PR values very close to the
ME3 ones).
4.7. Effective area
The total MECS effective area, Ae (E,theta), results from the
MU effective area (AMU), reduced by some transmission
coefficients related to the plasma protection grid (Tf1),
the plasma/UV filters (Tf2), the Be window (Tw), and to
the detector efficiency (Pa); a further reduction coefficient
(BLs) due to the Burst Length selection must be also
considered:
Ae(E,theta) = AMU,infi(E,theta)·Tf1
·
Tf2(E)·
Tw(E)·Pa(E)·BLs(E)
Fig. 11 shows the MECS (3 units) effective collecting area
as function of energy for different off-axis angles.
All the effective area components will be described in
the following sections. It is important to point out that,
during the on-ground calibration, measurements of the absolute efficiency have been done only for the optics. The
effects of the other components are evaluated mainly by
simulations.
4.7.1. Mirror efficiency and vignetting
The MU effective area is given by:
K·Adet
·
NMU / NFF ·
EFF / EMU ·
TFF / TMU
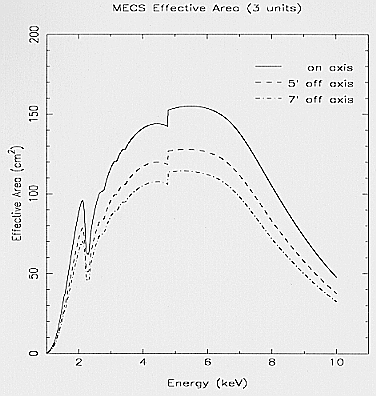 Fig. 11. The MECS effective collecting area as function of
energy for different off-axis angles
Fig. 11. The MECS effective collecting area as function of
energy for different off-axis angles
where NMU and NFF are the number of counts detected
during a Mirror Unit and a Flat Field measurements respectively,
TMU and TFF are the exposure times corrected
for the instrumental dead time,EMU and EFF indicate the
detector efficiency for MU and FF measurements respectively,
A det is the geometrical area of the detector, and
K is a correction factor taking in account the different
flux, on the detector and on the Mirror Unit, due to their
different distance from the X-ray beam source.
EFF is in general different from EMU . In fact, during
a FF measurement, the X-ray flux is spread on the entire Be
window and partially absorbed by the strongback
structure while, during a MU measurement, the X-ray flux
is well concentrated in a small region of the window due
to the optics spread function, and only for particular offaxis
angles it is absorbed by the strongback structure. The
difference between the two values EMU and EFF is significant below
a few keV while it becomes negligible above 4
keV.
NMU and NFF were computed by accumulating events
in selected energy intervals. The detector energy gain was
corrected for the position distortion by using the correction
maps (see Sect. 4.2), and for the time variation by
using the gain of the inner 55 Fe calibration sources.
The instrumental background, measured in a long detector exposure
with the X-ray beam switched off, was
subtracted from the accumulated events. Furthermore,
two regions of 3 mm radius around the inner 55Fe calibration sources
were excluded from the accumulation process.
For each PANTER calibration line (see Table 3) we
obtained a set of effective area values corresponding to
the different off-axis positions. Each set at energy E i was
fitted by the function:
A(Ei,theta) = A1(Ei)·V(Ei,theta)
where
V (Ei,theta) = [1 / (1 + A2(Ei) · thetaA3(Ei))]
is a vignetting factor with
theta = P [(Xj - Xj)2 + (Yj - Yj)2]½
where Xj and Yj are the baricenter coordinates (mm)
of the spot image during a MU measurement at off-axis theta,
Xo and Yo are the on-axis focal plane coordinates,
and P is the MECS plate scale factor. Xo, Yo, A1(Ei),
A2(Ei),
and A3(Ei) are free parameters of the fitting procedure.
A1(Ei), the maximum of the function, is the MU on-axis
effective area.
Fig. 12 shows the on-axis optics effective area for each
of the three MECS mirror units. The theoretical effective
area has been computed by considering the optics coned
geometry and the Au reflection coefficient (Henke et al.,
1993 ). The agreement between theoretical and experimental
results has been reached by multiplying the theoretical value
with a second order polynomial of energy.
The best polynomial parameters are obtained by fitting
experimental data; the result of the fitting, A(E,0), are
reported in Fig. 12 as a continuous line, while the diamond
markers represent the A1(Ei) values. The general
equation becomes:
A(E,theta) = A(E,0)·V(E,0)
For each energy Ei-1 < E < Ei, the
vignetting factor V(E,thete) is derived by interpolation of the experimental
values V(Ei-1,theta) and V(Ei,theta)
The results shown in Fig. 12 refer to the case of an
emitting source located at 130 m from the optics
(PANTER configuration). The finite distance of the source
produces a loss of effective area compared to the case in
which the emitting source is located at infinite distance.
In fact, for finite distance, the beam is divergent, and a
small but not negligible fraction of the radiation is imaged
in a region around the focus. This region appears as
a large radius annulus in the case of on-axis source
direction (theta = 0o ), and it assumes a more
complicated shape for
large theta values. The intensity of the loss radiation is
function of energy, too; being each mirror at different slope,
their contribution to the finite distance radiation loss are
different: high energy photons (E 6 keV) are reflected
mainly by the inner optics, while low energy photons by
the entire optics system.
To obtain the correct AMU,infi (E,theta) starting from the
A(E,theta) values, we simulated, by means of a ray-tracing
software, both the infinity case (parallel beam) and the
PANTER case (divergent beam) for several values of E
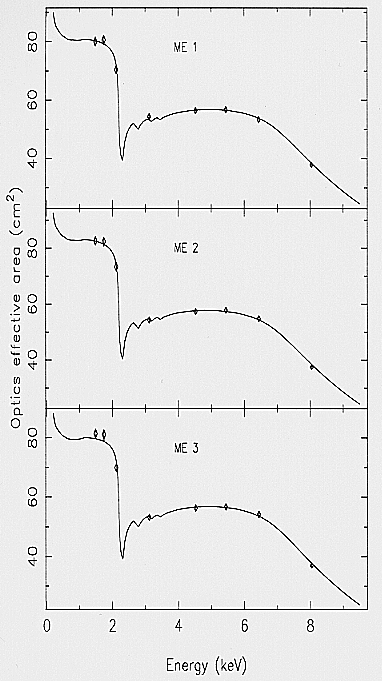 Fig. 12. On-axis optics effective area vs. energy for each MECS
unit. The diamond markers correspond to the A1(E i ) values
(see text). The continuous lines, A(E,0), represent the
theoretical expectation multiplied by a second order polynomial
Fig. 12. On-axis optics effective area vs. energy for each MECS
unit. The diamond markers correspond to the A1(E i ) values
(see text). The continuous lines, A(E,0), represent the
theoretical expectation multiplied by a second order polynomial
and theta. The optics geometry was followed in all its details
by the traced rays, and only the radiation reaching
the focal plane whithin a circle corresponding to the Be
window, was taken into account for the computation of
the effective area. Two different sets of values have been
produced, namely Ainfi(E,theta) and A130(E,theta). Finally, the
relation between AMU,infi and A(E,theta) can be written as:
AMU,infi(E,theta) = [A(E,theta)·Ainfi(E,theta)] /
[A130(E,theta)]
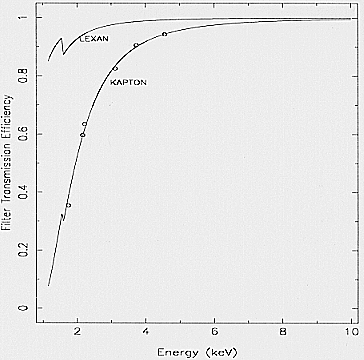 Fig. 13. LEXAN and KAPTON filter transmission efficiency
vs. energy. Circles indicate measured values (Jager, 1996)
Fig. 13. LEXAN and KAPTON filter transmission efficiency
vs. energy. Circles indicate measured values (Jager, 1996)
4.7.2. UV/ions shield windows
In order to avoid that the plasma particles crossing the
MU can accelerate towards the Be window set at -8 kV,
a plasma protection grid is mounted below the optics system.
The grid in Au-coated tungsten is kept at +28 V,
shielding the Be window electric field. This grid causes a
loss of effective area of 8% (Tf1 = 0.92), independent on
the energy. Furthermore, to be sure that any high velocity
plasma component overcoming the grid shielding doesn't
impinge on the Be window, plasma filters have been placed
in front of them. The filters stop also UV light photons
that could extract electrons from the Be window; these
electrons, accelerated by the Be window electric field
towards the MECS Carbon fiber walls, should produce a
background increase due to the electron bremsstrahlung
emission.
The first solution adopted for plasma/UV damage protection
was the use of thin Polyimide filters, as in the
LECS case (Parmar et al., this volume), and the MECS
on-ground PANTER calibrations were performed with
this kind of filter. Unfortunately, after vibration test, one
of the Polyimide filters was found to be destroyed. Now, in
the flight configuration, ME2 and ME3 units are both protected
by a LEXAN filter 0.6 -6m thick, aluminium plated
by two layers of 0.035 -6m, each; for precautionary reason,
the third unit, ME1, is protected by a 7.6 -6m
thick KAPTON filter, aluminium plated by two layers of 0.1 -6m,
each. Fig. 13 shows the transmission efficiency Tf2 for the
two filters.
4.7.3. Beryllium transmission
No measurements of the Be window transmission efficiency Tw
were performed during the MECS on-ground
calibrations; anyway, this efficiency can be computed
analytically by:
Tw = exp(-mu(E)·x)
where mu(E) is the absorption coefficient of the material
at the energy E, and x is the thickness. Fig. 14 shows the
transmission effciency for a layer of 50-6m
(window thickness) and for a
layer of 600 -6m (window plus strongback
thickness), representing the two different regions of the
detector window, as shown in Fig. 2 (verification
of strongback thickness from FF measurements is in progress).
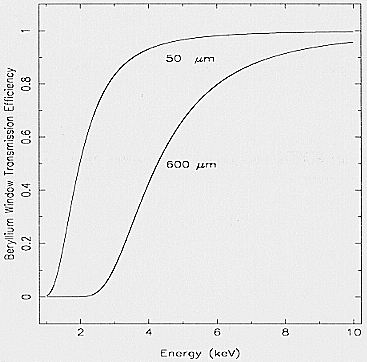 Fig. 14. Beryllium transmission efficiency vs. energy for two
different thickness values
Fig. 14. Beryllium transmission efficiency vs. energy for two
different thickness values
4.7.4. Detector efficiency and burst length selection
The gas cell absorption probability Pa is:
Pa = 1 - exp(-muXe(E)·D)
where muXe is the Xe absorption coefficient for the
energy E, and D is the size of the absorption region. Fig. 15
shows the gas cell efficiency obtained with D equal to the drift
region depth; events that convert in the scintillation
region are rejected to improve the energy resolution.
In Fig. 16 the BL versus energy pseudo-image (contour plot)
for the Cu line spectrum is shown. The spot
''a'' refers to events which convert in the drift region with
a single electron cloud giving correct PHA and BL values;
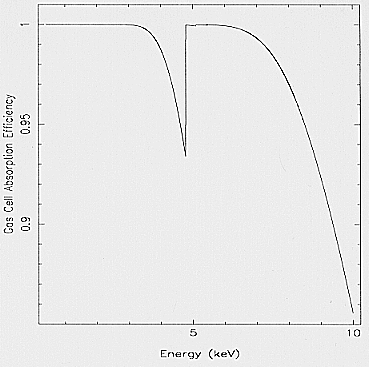 Fig. 15. Gas cell absorption efficiency for the drift region vs.
energy
Fig. 15. Gas cell absorption efficiency for the drift region vs.
energy
this kind of events make up more than 90% of the total
events. The spot ''b'' refers to the residual events; these
events present a single electron cloud too, but an incorrect
PHA value (see Sect. 4.3 for further details). The bridge
between ''a'' and ''b'' is mainly due to events that,
interacting with the Xenon near the Be window, loose part of
the electrons for attachment to that window. This phenomenon
is seen as a low energy tail in the line spectra
(as already explained in Sect. 4.3). The tail ''c'' is due to
events which are absorbed in the scintillation region
producing a reduced amount of UV light (and a shorter BL),
resulting in an incorrect PHA value due to the shorter
path in that region. These events, in the case of the Cu
line (8.06 keV), are 4.5% of the total number of events;
for lower energies, this fraction decreases due to a shorter
penetration depth (see Fig. 15). The jet ''d'' is due to
some of double events, i.e. to events with the fluorescence
photons re-absorbed inside the gas cell but at a different
position from the primary conversion. This effect produces
correct PHA value but a higher BL value due to the sum
of the two scintillation bursts; the position detected for
these events (2.4% of the total number) should be incorrect
being the weighted average of the two interactions.
The rejection of ''c'' and ''d'' events is performed by using
a suitable BL selection. Such a kind of picture is typical of
energies greater than 4.78 keV (the Xe L-edge); for
lower energies, the regions ''b'' and ''d'' disappear while
the ''c'' region becomes negligible. A BLs (E) function has
been derived to introduce the effect of the selection in the
MECS total effective area (Ae(E,theta)) computation.
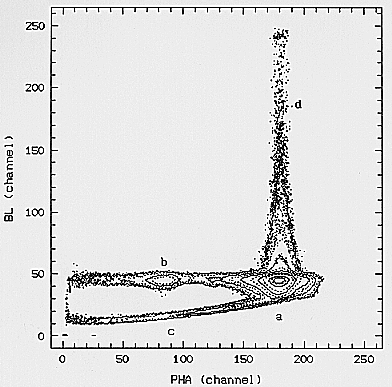 Fig. 16. Burst Length vs. energy pseudo-image for the Cu line
Fig. 16. Burst Length vs. energy pseudo-image for the Cu line
4.8. Background counting rate
Two components will be present in flight:
- the induced particles, and
- the diffuse X-ray, due essentially to the extragalactic
component. The galactic component, mainly at low energies,
is not detected because of the Be window transparency
(less than 5% below 1.0 keV).
Environmental charged particles, interacting with the
gas in the detector, loose their energy producing electron
clouds. The dimension of the clouds is generally bigger
than the one due to X-ray photons of equivalent energy,
because of the longer path the particle covers before being
stopped. The Burst Length, proportional to the cloud
dimension, can then be used to discriminate genuine photons
from charge induced events.
Measurements of the environmental background have
been performed during the PANTER and ESTEC calibration
campaigns. The longest background accumulation,
relative to the ME1 unit, has a duration of ~=9 hours.
Data used for the evaluation of the residual background
have been opportunely selected in BL and in position. Fig.
17 shows the image of the residual background after the
BL selection applied during the data analysis. The circle
indicates the region used for the analysis: the outer region
is not considered in order to exclude both the two spots
produced from the inner 55Fe calibration sources and the
high density outer ring; this ring is due to events
converting in the outer part of the detector (outside Be window
diameter) and compressed towards the internal region by
the readout system.
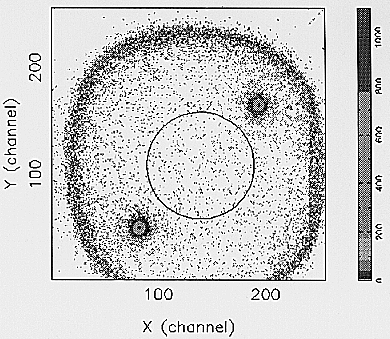 Fig. 17. Environmental background image. The circle delimits
the region for which are valid the data reported in Table 5
Fig. 17. Environmental background image. The circle delimits
the region for which are valid the data reported in Table 5
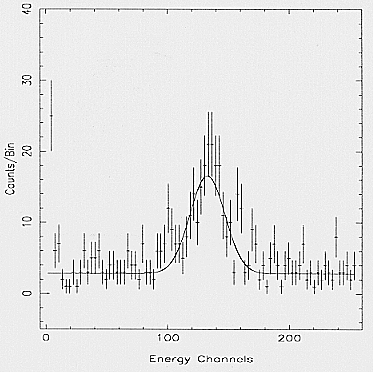 Fig. 18. Residual background spectrum within the circle as in
Fig. 17
Fig. 18. Residual background spectrum within the circle as in
Fig. 17
The spectrum of the selected events is shown in Fig. 18.
The spectrum was fitted with a constant plus a gaussian;
the results of the fit are shown in Table 5. A line-type
feature is evident in the central part of the spectrum. Possible
explanations of this feature are: a) fluorescence by detector
material (as the NiCo ring in Fig. 1); b) re-absorption, far
from the primary interaction point, of fluorescence emitted from
the 55 Fe calibration sources; c) combination of
the two above effects. The background is in any case very
low and the statistics collected during the on-ground cali
bration does not allow a conclusive analysis of the nature
of the line. A deeper analysis of the detector background
will be performed with the in-flight data.
Table 5. Background counting rate: results of the fit
| Parameter | Value |
| Flux of the constant | (4.95±0.59) 10-4 cts/cm2/s/keV
|
| Flux of the line | (13.5±1.3) 10-4 cts/cm2/s
|
| Energy of the line | 6.07±0.13 keV
|
| Line width | ~= 8.2 % (compatible with the detector resolution)
|
Estimation of the in-flight residual flux of charged
particle background from previously flown (EXOSAT)
and currently operating (ASCA) Gas Scintillation Proportional
Counters brings to a conservative value of 2·10-3
cts/cm2/sec keV in the 2 - 10 keV band.
Evaluation of the expected count rate from the extragaltic component
of the diffuse background has been made by simulating photons coming
from off-axis up to 1o with uniform angular distribution.
The spectrum used in
the simulation is a power law of spectral index 1.5 corrected,
at low energy, for the galactic absorption from
a column of 3·1020/cm2. The obtained count rate is
1.3·10-3/cm2/sec/keV, where cm2 is referred
to the considered detector area.
Acknowedgements
We wish to thank L. Scarsi for the effort he
spent in supporting BeppoSAX mission, R.C. Butler for his
tenacious interest in the scientific instruments, O. Citterio for
the work in developing the technology and the testing methods
of the Mirror Units, G. Manzo for the original contribution
to the design and development of the ME detector. G. Ferrandi,
E. Mattaini, and E. Santambrogio, from IFCTR Institute, provided
the mechanical calibration support equipment.
We thank H. Brauninger and W. Burkert for the support to
the calibration activity at the PANTER facility. L. Casoli, M.
Confalonieri, P. Dalla Ricca, T. Motta, A. Prestigiacomo, G.
Rimoldi, A. Sada, P. Sarra, and L. Vierbi, from Laben industry,
sub-contractors for the MECS instrument, assured the management
of the detectors and of the data acquisition system during
the calibration campaigns. S.Molendi acknowledges useful
discussions with H. Ebeling on PSF models. We wish thank K.
Ebisawa for the useful suggestions to improve this paper. All
the activities of the Scientific Institutes have been financially
supported by the Italian Space Agency (ASI) in the framework
of the BeppoSAX mission.
References
- Boella, G. et al. 1995, Proc. SPIE Conference, San Diego, CA, USA, Paper n. 2517-14
- Boella, G. et al. 1996, this volume
- Butler, C., Scarsi, L. 1990, SPIE 1344, 46
- Citterio, O. et al. 1985, SPIE 597, 102
- Citterio, O. et al. 1988, Appl. Opt. 27, 1470
- Conti, G. et al. 1993, SPIE 2011, 118
- Conti, G. et al. 1994, SPIE 2279, 101
- Dos Santos, J.M.F., Conde, C.A.N., Bento, A.C.S.S.M. 1993, NIM A324, 611
- Henke, B.L., Gullikson, E.M., Davis, J.C. 1993, Atomic Data and Nuclear Data Tables 54, 2
- Inoue, H. et al. 1978, NIM-PR 157, 295
- Jager, R. 1996, private communication
- Lamb, P. et al. 1987, Astrophysics and Space Science 136, 369
- Molendi, S. et al. 1995, Proc. Int. Conf. on X-Ray Astronomy and Astrophysics, W®urzburg, Germany, in press
- Parmar, A.N. et al. 1996, this volume
- Ramsey, B.D. et al. 1994, Space Science Rev. 69, 139
- Santos, F.P. et al. 1991, NIM A307, 347
- White, N.E. 1985, EXOSAT Express 11, 51
