|
NOTICE:
This Legacy journal article was published in Volume 5, November 1994, and has not been
updated since publication. Please use the search facility above to find regularly-updated information about
this topic elsewhere on the HEASARC site.
|
Calibrating BBXRT
K. A. Weaver
Penn State University
1. Overview
This article summarizes the calibration of the two solid state Si(Li) X-ray
detectors and the X-ray telescopes that flew as part of Goddard Space Flight
Center's Broad-Band X-Ray Telescope (BBXRT) experiment on board the space
shuttle Columbia in 1990 December. BBXRT was a precursor of ASCA, and
consisted of two identical telescopes with lightweight, nested, thin-foil
conical imaging mirrors (Serlemitsos 1988), which focused X-rays onto two
segmented spectrophotometric Si(Li) diodes located at the focal plane. During
its flight, BBXRT spent roughly 185,000 secs pointing at celestial sources with
typical integration times of 500 to 2,000 secs. The BBXRT observation log,
containing a complete list of all scientifically useful pointings, can be found
in Weaver et al. (1995). This article contains useful information for anyone
wishing to analyze BBXRT data, such as discussions of the effective area and
flux calibrations, flux corrections for off-axis observations, background
subtraction techniques for daytime observations, and the systematic
uncertainties in the effective area calibration for point sources. For details
of the instrument and in-flight performance see Weaver et al. (1995) and Smale
(1992).
2. The BBXRT Detectors, Mirrors, and Point Response Function
Each BBXRT detector, designated by "A" or "B", consisted of a silicon block
with a grooved surface, segmenting it into 5 spatial elements or "pixels" (Fig.
1). The grooves were 0.5 mm wide and were covered with an opaque mask that
also occulted 0.5 mm of the detector on either side of the groove. The radius
of the central pixels (designated A0 or B0) was 5 mm giving a field of view of
3.6 arcminutes, and the total diameter including the outer pixels was 19 mm or
17.3 arcminutes. The central detector elements had about 1/4 of the background
of the outer elements as well as an on-orbit energy resolution of approximately
100 eV FWHM at 0.9 keV and ~155 eV FWHM at 6 keV, while the outer pixels had a
slightly poorer resolution of ~170 eV FWHM at 6 keV. The signal processing
electronics gave each pixel 512 energy channels with widths of ~16 eV from
channels 1 to 255 and ~32 eV from channels 256 to 511. Because of the
low-energy noise threshold, the lowest usable channels in A0 and B0 are channel
16 and channel 17, respectively, which corresponds to about 0.3 keV. This
ranges from channels 25 to 30 in the outer pixels, which corresponds to ~0.4
keV (Table 1).
Figure 1 illustrates the approximate orientation of the BBXRT detectors with
respect to the aspect camera and projected onto the celestial sphere. The
outer pixels of the A detector are labeled A1 to A4 counterclockwise on the
sky. The telescope roll angle,
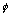 increases counterclockwise and is defined such that when
increases counterclockwise and is defined such that when
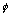 =
0, the top of the camera and the top of pixel A4 point north. The B detector
is rotated by 180 degrees with respect to the A detector such that A1 and B3
observe the same area of the sky. Postflight analysis indicates a slight
offset between the A and B telescopes (not shown in Fig. 1). The mean
displacement of B from A is 0.822 arcminutes at an azimuth of -63.24 degrees.
This azimuth is measured arbitrarily from the B3/B4 boundary and represents a
63 degree rotation through B4 toward B1. Because the the A system axis was
taken as the nominal pointing position of the telescope, this displacement
generally leads to a lower count rate in the B detector. A correction to
account for the difference in observed count rates between A and B is not
included in the effective area calculations. Therefore, all fluxes are
measured with respect to the A system. Here, the term "on axis" refers to a
source centered in the A detector. =
0, the top of the camera and the top of pixel A4 point north. The B detector
is rotated by 180 degrees with respect to the A detector such that A1 and B3
observe the same area of the sky. Postflight analysis indicates a slight
offset between the A and B telescopes (not shown in Fig. 1). The mean
displacement of B from A is 0.822 arcminutes at an azimuth of -63.24 degrees.
This azimuth is measured arbitrarily from the B3/B4 boundary and represents a
63 degree rotation through B4 toward B1. Because the the A system axis was
taken as the nominal pointing position of the telescope, this displacement
generally leads to a lower count rate in the B detector. A correction to
account for the difference in observed count rates between A and B is not
included in the effective area calculations. Therefore, all fluxes are
measured with respect to the A system. Here, the term "on axis" refers to a
source centered in the A detector.
BBXRT used 10 cm long conical reflectors that approximated a Wolter type I
mirror optical system. There were two adjacent, coaxial, and confocal arrays
of cones in each mirror assembly. The mirror performance is summarized by
Petre et al. (1992), and the mirror fabrication techniques and mirror
parameters are described in detail by Serlemitsos (1988) and Serlemitsos et al.
(1991). The point spread function (PSF) of the mirrors is broader than a
single Gaussian profile. For a source observed on axis ~62% of the counts that
reach the detector fall in the central pixel, ~21% fall on the mask between the
pixels, and ~17% fall into the outer pixels (Smale 1992). For a source
observed near the edge of a pixel or on the mask, a larger fraction of photons
is lost to the mask (up to 50%). It is necessary to correct for this loss when
measuring absolute fluxes (see Section 3.3). A possible energy dependence of
the PSF is discussed in Section 3.4.3.
Figure 1
Table 1: Reliability of Response Matrix at Low Energies
Pixel Lowest available Energy Lowest reliable Energy
pha channel (keV) pha channel (keV)
A0 16 0.29 16 0.29
A1 26 0.41 26 0.41
A2 26 0.42 26 0.42
A3 27 0.44 27 0.44
A4 25 0.41 43 0.70
B0 17 0.30 17 0.30
B1 27 0.42 39 0.60
B2 28 0.43 34 0.52
B3 28 0.45 34 0.54
B4 29 0.44 45 0.69
3. Calibration of the Detectors and Mirrors
3.1. Incomplete charge collection uncertainties
The term "incomplete charge collection" refers to charge loss mechanisms in the
detector that result in an underestimation of the incident photon energy.
Incomplete charge manifests itself as non-Gaussian components that occur in the
response function below the main Gaussian photopeak. The shapes and magnitudes
of these components vary from detector to detector (Shima et al. 1983), but
they are difficult to model because their physics is poorly understood.
For simplicity, we initially modeled the incomplete charge in the BBXRT
detectors as a step function (convolved with a Gaussian) starting at the energy
of the incident X-ray and extending to zero energy. However, we found that (1)
there was a significant incomplete-charge tail that rises toward low energies
(<0.7 keV), (2) the tail was a larger effect in the calibration data than in
the flight data, and (3) the tail was a larger effect in the outer B pixels
than in the outer A pixels. Because the tail differs between flight and
calibration data, we require fitting celestial sources to measure it. However,
because of the uncertainties inherent in fitting the Crab to determine its
magnitude, we have not included the tail in our response function. This lack
of a correct model of the incomplete charge collection causes an uncertainty in
the low-energy effective area calibration of the outer B pixels.
3.2. Data from the Crab Nebula
Observations of the Crab Nebula were made four times during the mission. Light
curves of the day 3 observation in the A pixels are shown in Figure 2. The
Crab Nebula was first observed for 2,300 seconds at ~3.0 arcminutes off axis,
with the source flux highest in pixels A1 and B3. An attitude adjustment that
began at 3.054 days mission elapsed time (MET) placed the Crab in pixels A0 and
B0. This observation is designated "on axis" for calibration purposes,
although the Crab was offset by about 1 arcminute toward pixel A3. The first
half of the on-axis observation was performed during orbit night, while the
second half was performed during orbit day.
Figure 2
The Crab Nebula X-ray spectrum can be well described by a single absorbed power
law over the 1-10 keV energy band. The photon index is well known, with the
average value in the literature being 2.1. There is, however, some
disagreement over the observed value of the hydrogen column density along the
line of sight to the Crab. The measured values for
NH are
not all consistent, and the discrepancy is rather high in a few cases (see
e.g., Seward 1992; Weaver 1993, Table 3.4). The mean value of the column
density from the literature is
NH = (2.9 +/- 0.4) x 1021 cm-2.
Complexities in the Crab's spectral and spatial characteristics have been
observed at both high and low energies. The spectrum flattens at high energies
due to the contribution from the pulsar. This effect is ~10% at 10 keV (Toor
and Seward 1977). Below 2 keV, the angular size of the Crab increases. This
is attributed to interstellar dust that causes low energy photons to be
scattered into a dust halo. In fact, 11% of the total 0.5-3.5 keV flux
measured with the Einstein Observatory IPC appears at a radius of greater than
1.6 arcminutes (Mauche and Gorenstein 1989). However, from a comparison of
Crab spectra between pixels, we conclude that any effects of the
dust-scattering halo are less than the ~15% uncertainty in the hydrogen column
to the Crab, so for simplicity we did not include a dust scattering halo in our
calibration model. The effective areas for the two central pixels was refined
based on fitting the on-axis Crab spectrum to an absorbed power law with a
photon index of 2.10 and a neutral hydrogen column density of
3 x 1021 cm-2.
3.3. The Mirror Areas and Flux Corrections
To obtain the 2-10 keV assumed Crab slope, we allowed the density of
vacuum-deposited gold on the mirrors to be a free parameter in the effective
area calculations. The mirror areas were then generated for the entire focal
plane. For simplicity, we chose to fit the Crab data from the central pixels
only under the assumption the the PSF is independent of energy. However, our
assumption that energy-dependent scattering by the mirrors is not important may
be incorrect (Section 3.4.3).
Two vignetting corrections are currently included in the BBXRT response matrix.
First, the effective area curve is normalized by 62% under the assumption that
one is analyzing data from the A0 pixel for an on-axis source. This correction
factor accounts for 38% of the source counts being lost, primarily to the mask
and the outer pixels (Section 2), and provides accurate fluxes for sources that
are more or less centered in A0. Second, for off-axis sources,
energy-dependent vignetting corrections to the effective area are included in
the response. These were obtained by modeling the throughput of the mirrors as
a function of off-axis angle using ray-tracing techniques (Weaver et al. 1995,
Fig. 10). The ray-tracing calculations have been performed for point sources
only.
A third correction that has not been included in the response matrix accounts
for the (often significant) loss of photons for sources observed off axis due
to the presence of the masks between the detector elements. If a source
happens to sit directly over a mask, up to 50% of the photons reaching the
focal plane can be lost. As an illustration of the potential severity of the
problem, the distribution of photons in the focal plane for a point source
observed in three different locations is shown in Figure 3. Here, the
azimuthal angle
 ,
is arbitrarily measured with respect to the edge of the outer pixel nearest the
source position and increases toward the center of that pixel. Due to the
symmetry of the outer pixels, ,
is arbitrarily measured with respect to the edge of the outer pixel nearest the
source position and increases toward the center of that pixel. Due to the
symmetry of the outer pixels,
 ranges from 0 degrees to 45 degrees. Case (a) illustrates the distribution of
photons for a point source that is directly on axis. For a source that is
located 4 arcminutes off axis and directly over the mask (case b), the total
collection efficiency is cut by one half. However, in case (c), where the
source is off axis but centered in an outer pixel the total collection
efficiency is higher than in case (a) due to the larger size of the outer
pixels. Ray-tracing techniques have been used to calculate the fraction of
counts lost to the mask for a multitude of source positions. Figure 4 provides
the flux-correction factor to be used for off-axis observations for sources
having off-axis angles
ranges from 0 degrees to 45 degrees. Case (a) illustrates the distribution of
photons for a point source that is directly on axis. For a source that is
located 4 arcminutes off axis and directly over the mask (case b), the total
collection efficiency is cut by one half. However, in case (c), where the
source is off axis but centered in an outer pixel the total collection
efficiency is higher than in case (a) due to the larger size of the outer
pixels. Ray-tracing techniques have been used to calculate the fraction of
counts lost to the mask for a multitude of source positions. Figure 4 provides
the flux-correction factor to be used for off-axis observations for sources
having off-axis angles
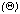 ranging from 0 arcminutes to 8 arcminutes and azimuthal angles of
ranging from 0 arcminutes to 8 arcminutes and azimuthal angles of
 = 0.0 degrees, 22.5 degrees, and 45 degrees.
= 0.0 degrees, 22.5 degrees, and 45 degrees.
To determine the flux for an off-axis point source,
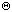 and
and
 must be known. If an aspect solution is available, the R.A. and Decl. offsets
and the roll angle (Weaver et al. 1995, Table 1) provide both angles.
Otherwise,
must be known. If an aspect solution is available, the R.A. and Decl. offsets
and the roll angle (Weaver et al. 1995, Table 1) provide both angles.
Otherwise,
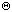 and
and
 can be estimated by utilizing a ray-tracing program (currently known as KNIFE[1]) available from the HEASARC. Figure 4 gives
the appropriate correction to the fluxes derived with the BBXRT response
matrix. For example, for a point source having
can be estimated by utilizing a ray-tracing program (currently known as KNIFE[1]) available from the HEASARC. Figure 4 gives
the appropriate correction to the fluxes derived with the BBXRT response
matrix. For example, for a point source having
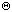 = 5 arcminutes and
= 5 arcminutes and
 = 45 degrees, the flux correction factor for the A detector pixel in which the
source is located (the source pixel; labeled as "pixel 1" in Figs. 3 and 4) is
1.23. The flux-correction factor for each of the adjoining or "nonsource"
outer pixels (labeled as "pixel 2" and "pixel 4" in Figs. 3 and 4) is ~0.02.
To derive the flux of the source, divide the apparent flux derived from the
spectral fit by the flux-correction factor for that pixel.
= 45 degrees, the flux correction factor for the A detector pixel in which the
source is located (the source pixel; labeled as "pixel 1" in Figs. 3 and 4) is
1.23. The flux-correction factor for each of the adjoining or "nonsource"
outer pixels (labeled as "pixel 2" and "pixel 4" in Figs. 3 and 4) is ~0.02.
To derive the flux of the source, divide the apparent flux derived from the
spectral fit by the flux-correction factor for that pixel.
Figure 3
3.4. The Effective Area Curve
The effective area curves for the central pixels were generated by allowing the
optical depths of the various sources of absorption within and above the
detectors (Si, C, Al, Au) to be free parameters in fits to the Crab. Details
of the procedure are given by Weaver (1993). Although the Crab was not
observed in all pixels, other bright sources such as Cygnus X-1, Cygnus X-2,
and Perseus were available for calibrating the outer pixels. The effective
area curves for the outer pixels were calculated by fitting their spectra
simultaneously with an A0 or B0 spectrum of the same source and varying the
absorption parameters (and the magnitude of incomplete charge within certain
limits) to give the best fit. After the absorption parameters were adjusted,
the effective area curve still underpredicted the Crab data at greater than 6
keV. This high-energy tail was a 20% effect in both A0 and B0 at 10 keV, more
than the 10% flattening expected due to the presence of the pulsar. The excess
of photons at high energies has been corrected by multiplying the effective
area by a relation of the form R = m x E + b above
05.2 keV, where m is 0.0429 and 0.055 for A and B respectively, and
b is 0.772 and 0.708 for A and B, respectively.
Figure 4 a, b, and c
3.4.1. On-axis Observations
Figure 5a illustrates the best power-law fit to the on-axis A0 Crab
observation, which results in
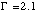 and NH = 3 x 1021 cm-2.
The residuals are shown in Figure 5b. Figure 6a shows the best power-law fit
to the on-axis observation in B0 which also results in
and NH = 3 x 1021 cm-2.
The residuals are shown in Figure 5b. Figure 6a shows the best power-law fit
to the on-axis observation in B0 which also results in
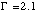 and NH = 3 x 1021 cm-2.
The residuals are shown in Figure 6b. Close inspection reveals that fewer
counts are observed in the B detector than in the A detector below about 2-3
keV. This occurs for all B detector elements and appears to be due to the B
detector being covered with a thicker gold surface contact layer than the A
detector.
and NH = 3 x 1021 cm-2.
The residuals are shown in Figure 6b. Close inspection reveals that fewer
counts are observed in the B detector than in the A detector below about 2-3
keV. This occurs for all B detector elements and appears to be due to the B
detector being covered with a thicker gold surface contact layer than the A
detector.
At the present time, the effective area is understood at the 5% level in A0
with up to 10% residuals at very low energies (<0.6 keV). The area is also
understood at the 5-10% level in B0 over the 0.6 to 9 keV range. However,
residuals to the Crab in B0 appear both below 0.6 keV and above 9 keV at the
10-15% level. The ~10% residuals above 9 keV appear to be due to incomplete
modeling of the 8.3 keV edge caused by the nickel mesh in front of the
detector. There is also a larger mismatch to the Al, Si, and Au edges in B0
than in A0, and there is a narrow feature present at 1.38 keV in B0. This
feature is at worst a 10% residual, and less than 10 eV equivalent width when
fit with a Gaussian. In addition, a <5% "bump" in the residuals still
exists around 7.5 keV in both A and B.
The worst residuals in both detectors are at ~0.5 keV. When the on-axis Crab
data are split into night and day, there is an indication that the low-energy
residuals change with time, ranging from a 5% to a 15% effect. It appears that
they are caused by a temporal change in the gain or low-energy resolution. The
magnitude of the residuals can be measured as follows: fitting the positive
~0.5 keV feature with a narrow Gaussian (E = 0.41 keV) gives an equivalent
width of less than 140 eV in A0 and less than 220 eV in B0. Fitting the
negative feature gives an energy of 0.52 keV (a slightly lower energy than an
oxygen edge at 0.53 keV). Fitting with a notch (width 0.03 keV) gives a
covering fraction for the notch of <0.4 for A0 and <0.65 for B0.
Figure 7 shows the confidence contours for NH
versus
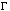 derived from all pixels when the Crab is approximately on axis. The 90%
confidence contours for A0 and B0 overlap, indicating that the two central
pixels (the source pixels) give consistent results for the Crab. However, for
the outer pixels (the nonsource pixels), the remaining systematic uncertainties
derived from all pixels when the Crab is approximately on axis. The 90%
confidence contours for A0 and B0 overlap, indicating that the two central
pixels (the source pixels) give consistent results for the Crab. However, for
the outer pixels (the nonsource pixels), the remaining systematic uncertainties
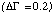 are
2 to 3 times greater than the statistical uncertainties in fitting the Crab.
The systematic uncertainty measured in the outer pixels may be because we have
not accounted for an energy dependence in the the mirror PSF (Section 3.4.3). are
2 to 3 times greater than the statistical uncertainties in fitting the Crab.
The systematic uncertainty measured in the outer pixels may be because we have
not accounted for an energy dependence in the the mirror PSF (Section 3.4.3).
3.4.2. Off-axis Observations (Source Pixel)
There are remaining uncertainties for outer pixel data. Although most of the
outer A pixels are reliable down to their lowest usable energies (Table 1), the
A4 pixel is particularly noisy and so is only reliable down to about 0.7 keV.
Also, because of the uncertainty in modeling the incomplete charge collection,
the outer B pixels are reliable only to 0.5-0.7 keV.
The confidence contours for NH versus
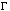 for all pixels when the Crab is 3.0 arcminutes off axis are shown in Figure 8.
In this case, the source pixels are A1 and B3. The index measured for A1
for all pixels when the Crab is 3.0 arcminutes off axis are shown in Figure 8.
In this case, the source pixels are A1 and B3. The index measured for A1
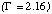 is steep and is inconsistent with the index measured for B3
is steep and is inconsistent with the index measured for B3
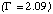 .
This represents the largest discrepancy still remaining between pairs of
source pixels .
This represents the largest discrepancy still remaining between pairs of
source pixels
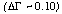 ,
although this should be an observable problem only for bright sources (greater
than or equal to ~10 counts sec-1) with good statistics. The
remaining discrepancy
between A1 and B3 is smaller than the general systematic uncertainties observed
between outer, nonsource pixels when the Crab is on axis (Fig. 7). ,
although this should be an observable problem only for bright sources (greater
than or equal to ~10 counts sec-1) with good statistics. The
remaining discrepancy
between A1 and B3 is smaller than the general systematic uncertainties observed
between outer, nonsource pixels when the Crab is on axis (Fig. 7).
3.4.3. On- and Off-Axis Observations (Nonsource Pixels)
For a point source observed with BBXRT, there are still large systematic
residuals when attempting to use data that are not from the source pixel.
During the on-axis observation, the Crab was actually offset by about 1
arcminute toward A3 and B1 (Section 3). From Figure 9, it can be seen that for
this observation, for 5 out of 6 of the pixels other than A0, B0, A3, and B1
(i.e., those pixels in which the majority of the Crab flux is coming from a
region greater than 5 arcminutes away from the core of the PSF), the spectra
tend to be flatter. The effect is even more obvious during the off-axis Crab
observation (Fig. 8). In this case, the source pixels are A1/B3 and A0/B0,
while A3/B1 are the furthest from the source in detector coordinates. Clearly,
the measured photon indices become much flatter with increasing angular
distance from the Crab.
The flattening in the Crab spectrum observed in nonsource pixels is due to the
increased presence of a high-energy tail in data obtained from a greater than 5
to 6 arcminute radius away from the center of the source in detector
coordinates. This flattening can be seen in power-law fits to data from the
outer pixels when the Crab is observed approximately on axis. Figure 9 shows a
plot of the ratio of the A2 and B4 Crab spectra to an absorbed power law model
having an index of
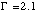 .
In this case, the best-fit NH
is the "expected" value of 3.0 x 1021 cm-2.
A tail at high energies (which is a 20% effect) is observed in the ratio of
the data to the model. .
In this case, the best-fit NH
is the "expected" value of 3.0 x 1021 cm-2.
A tail at high energies (which is a 20% effect) is observed in the ratio of
the data to the model.
Figures
5a and b
Figures
6a and b Figure 7
Figure 8
Figure 9
One
explanation for the high energy tail seen in the nonsource pixels is an
energy dependence of the mirror point response function for large radii.
Measurements appropriate to test for an energy dependence are not
available for the BBXRT mirrors. However, this effect has been observed
for the ASCA mirrors (H. Kunieda and the ASCA calibration team, 1993
private communication). Preliminary measurements of the ASCA mirrors
indicate that 7% of the flux at 2 keV, 15% of the flux at 5 keV, and 17%
of the flux at 8 keV is scattered from the core of the mirror PSF into a
greater than 6 arcminute radius (thus extending the wings of the PSF for
higher energies). This energy-dependent scattering has the right
magnitude to explain the high-energy tail observed in the outer-pixel
BBXRT data when the Crab is centered (Fig. 9), although off-axis
measurements of the Crab indicate that this tail is an even larger effect
than expected for a simple energy dependence of the PSF.
Recall
that we used only the A0 data (essentially from the beam core) to modify
the effective area to fit the Crab (Section 3.3). However, if scattering
out of the beam core is energy dependent, then a larger fraction of
high-energy photons than low-energy photons are scattered out of the core.
This means that the measured slope of the Crab when using only central
pixel data should be "too steep". We may have inadvertently corrected for
this steepening by altering the mirror gold density by ~5%. Therefore, it
is likely that our calibration contains a systematic error in the sense
that measured spectral slopes will be too flat by about 5 to 10% in 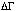 when using data
from a source pixel, whether the source is observed on or off axis.
However, this small effect should only be noticeable for sources having
count rates greater than ~10 counts sec-1.
For data from a nonsource pixel, the systematic flattening at high energies
can easily dominate statistical uncertainties for most point sources (Figs. 8
and 9). when using data
from a source pixel, whether the source is observed on or off axis.
However, this small effect should only be noticeable for sources having
count rates greater than ~10 counts sec-1.
For data from a nonsource pixel, the systematic flattening at high energies
can easily dominate statistical uncertainties for most point sources (Figs. 8
and 9).
4. Flux Calibration
To determine the normalization of the BBXRT effective area curve using the Crab
Nebula, corrections must be applied to the observed count rate because some
X-ray events are not recorded in the telemetry. The effects of dead time (see
Smale 1992), flagging, and pulse pile-up were examined using all of the events
in the telemetry for a one second interval for the on-axis A0 Crab observation
at 3.056 days. After correcting the observed count rate for these effects, we
find R_{obs}(spectrum) = 0.648 R_{true}. An absorbed power-law fit to the
on-axis Crab observation in A0 gives a normalization of
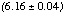 photons sec-1 keV-1 cm-2 at
1 keV (90% confidence errors). After applying the above correction, this
results in
photons sec-1 keV-1 cm-2 at
1 keV (90% confidence errors). After applying the above correction, this
results in
N(E) = 9.51 E-2.11 e( (E)NH) (E)NH)
where N(E) is given in photons sec-1 keV-1
cm-2.
Our derived normalization at 1 keV agrees well with the normalizations
measured by previous experiments (Toor and Seward 1974; Burrows 1982; Turner et
al. 1989), and indicates that our Crab flux is accurate to within ~15%.
This flux calibration applies only to sources observed on axis in the A
detector. To account for the mask for off-axis observations, one must apply a
flux correction factor (Section 3.3).
5. The Detector Background
There are four major contributions to the BBXRT detector background: internal
background, particles, events from the diffuse X-ray background (DXRB), and
X-ray contamination at low energies from solar radiation scattered off Earth's
atmosphere. This "Earthglow" is the dominant low energy component for daytime
observations, and its intensity correlates with the "Earth angle", defined as
the angle between the telescope pointing direction and the direction of the
center of the Earth. During nighttime observations, the instrumental background
and the DXRB contribute equally at low energies. See Weaver et al. (1995) and
Smale (1992) for a discussion of background rejection techniques.
5.1. The Non-X-Ray background
The non-X-ray detector background is made up of electronic noise, microphonics,
and particle events. Electronic noise is forced to be a small effect by
setting the discriminator thresholds above ~0.3-0.5 keV. Microphonics are
different from noise associated with the ordinary detector leakage current, and
bursts of microphonics events which typically last about 2 milliseconds can be
eliminated during data extraction for weak sources (Smale 1992).
Particle events are the primary source of the non-X-ray background. The
outer-pixel count rates for the non-X-ray background (from times when BBXRT was
not passing through the South Atlantic Anomaly [SAA]) are plotted against the
detector guard rate[2] in Figure 10. A
correlation between count rate a guard rate is clearly present, and it is
approximately linear for guard rates greater than about 1000 and less than
about 2000. This correlation allows the non-X-ray component of the background
to be easily predicted for a known guard rate. Below a guard rate of 1000, the
non-X-ray background reaches a lower threshold at about 0.15 and 0.18 counts
sec-1
in the summed outer A pixels and B pixels, respectively. The magnitude of the
non-X-ray background (excluding microphonics) is
1.5 x 10-3 counts keV-1 sec-1
in each central pixel and ~8 x 10-3
counts keV-1 sec-1 in
each outer pixel, with the exception of A4 which has a very strong non-X-ray
background component below 0.7 keV.
Figure 10
5.2. The Diffuse X-Ray Background during Orbit Night
For nighttime source observations and Earth angles greater than 90 degrees, the
external X-ray background is due solely to the DXRB. For a guard rate of
~1000, the count rate in the DXRB is approximately equal to the non-X-ray
background count rate over 0.4-0.6 keV, and can be one half the non-X-ray
background count rate over 0.6-1.0 keV. However, the DXRB flux is less than
10% of the non-X-ray background at energies greater than 2 keV. The diffuse
background count rate remains roughly the same for all observations because
BBXRT is not particularly sensitive to spatial fluctuations in the DXRB due to
short integration times.
5.3. The Atmosphere and the X-Ray-Bright Earth
The shuttle's orbit places it in Earth's upper atmosphere at an altitude of
~200 km. At this altitude, BBXRT suffers from a large amount of low energy
(0.3-1.0 keV) contamination during "day-side" observations. This contribution
to the X-ray background occurs when X-ray photons from the solar corona are
scattered by Earth's upper atmosphere. The relevant processes involved are
Thomson scattering and fluorescent scattering. BBXRT encountered two states of
bright Earth emission: an "active" state when the Sun was flaring and a
"quiet" state when the Sun was more or less quiescent. During the active
state, when the Sun emits higher energy photons, emission lines of Mg, Si, and
Ar are observed as well as a strong thermal continuum and Fe L emission.
Fortunately, no flares occurred during daytime source observations. During the
quiet state, we see a weaker thermal continuum and scattered Fe L emission as
well as O and N_2 fluorescence lines.
Figure 11 illustrates how the <2 keV bright Earth count rate changes with
Earth angle. The channel range 27-42 emphasizes the oxygen line, which is
brightest at Earth's limb (between 70-80 degrees). There is a large drop in
the count rate above 80 degrees although oxygen contamination persists up to
150 degrees. Channels 45-80 emphasize the change in the Fe L count rate with
distance from Earth's limb. There is once again a rapid drop above 80 degrees,
although there are significant counts in the Fe L complex even at 100 degrees.
For higher energies (channels 80-120), there is essentially no contribution to
the background for Earth angles larger than 80 degrees.
Figure 11
6. Background Subtraction
The non-X-ray component of the BBXRT background can be easily predicted as
follows. First, the average guard rate during the source observation (the
"source guard rate" or SGR) is determined (see Weaver et al. 1995, Table 1, for
a listing of guard rates). Second, the count rate of the non-X-ray background
(which has a mean guard rate, MGR, of 1259) is altered by a "background scale
factor", BSF = MGR/SGR, to match the count rate that is predicted from the
linear relation in Figure 10. Finally, the scaled background is subtracted
from the source data. The non-X-ray background reaches a lower threshold at a
guard rate of 1000 and should not be scaled below this value. The background
subtraction procedure discussed here only applies to observations out of the
SAA with an average accumulated guard rate of less than or equal to ~1400.
Creating an appropriate background for an observation obtained during orbit
night consists of adding together (1) a DXRB spectrum which has its non-X-ray
background already subtracted and (2) the non-X-ray detector background scaled
as described above. An appropriate background spectrum for a daytime
observation consists of (1) the daytime background (which contains scattered
light plus the DXRB) accumulated for the average Earth angle of the source
observation, minus its non-X-ray background, plus (2) the non-X-ray detector
background that has been scaled as described above.
The adopted background subtraction algorithm is given below. Here,
BGN is the nighttime (diffuse only) background, BGI
is the non-X-ray background, BGD(EA) is
the daytime (diffuse plus scattered) background as a function of Earth angle,
NGR (= 1274) and DGR (see Table 2) are the average guard rates of the nighttime
and daytime backgrounds, respectively, and SGR is the average guard rate during
the source observation. Night background, non-X-ray background, and daytime
background files for various Earth angles have already been extracted and are
available through the HEASARC for those wishing to use the following algorithm
to construct backgrounds appropriate for their observations.
BBXRT background subtraction algorithm:
ORBIT NIGHT:
Data - BGN - BGI (scaled using MGR/NGR)] -
BGI (scaled using MGR/SGR);
ORBIT DAY:
Data - BGD(EA) - BGI(scaled using MGR/DGR)] -
BGN(scaled using MGR/SGR).
Because BBXRT has five detector elements, the estimation of background is
fairly straightforward for weak point sources observed on axis. In this case,
the simultaneous outer-pixel data provide a direct estimate of the background
during the observation.
Table 2: Parameters for Daytime Backgrounds:
BGD(EA)
Earth Angle range DGR BSF
(degrees)
30-50 1066 1.18
50-70 1060 1.19
70-80 1033 1.22
80-90 1229 1.02
90-100 1126 1.12
100-110 1228 1.03
110-120 1210 1.04
120-130 1209 1.04
130-150 1225 1.03
150-180 1010 1.25
7. Remaining Systematic Uncertainties
We currently understand the BBXRT effective area curve at the 5-10% level
between 0.7-10 keV and at the 10-15% level below 0.7 keV for data from a source
pixel for both on- and off-axis observations of point sources. Further
refinements of the effective area await postflight ground calibration
measurements. A summary of the remaining calibration uncertainties are listed
below.
(1) Our step-function incomplete charge model does not properly account for the
low energy (<0.7 keV) shape of the incomplete charge distribution. This
mainly affects the B detector, and causes data from less than 0.6-0.7 keV in
pixels B1, B2, B3, and B4 to be unusable.
(2) A high-energy excess still exists in the B0 pixel above 9 keV (a ~10%
effect). This is probably due to incorrect modeling of the Ni edge at 8.3
keV.
(3) Low-energy residuals in the Crab data are seen. These may vary with time
and are a 5-15% effect below 0.6 keV.
(4) Residuals still remain around the Al, Si, and Au edges due to a mismatch of
our model to the Crab data (a 5% effect).
(5) Because we have not accounted for any energy-dependent scattering by the
mirrors, there is likely a systematic error for on-axis sources that causes the
2-10 keV slopes in A0 and B0 to be too flat by about 5-10%. This should only
be significant for bright targets.
(6) The systematic error in the measurement of the Crab slope between pairs of
outer pixels (for source pixels) is +/-0.10 in photon index.
(7) The measured power-law indices for Crab spectra from non-source pixels are
too flat by 10-25%. This is a greater than or equal to a ~10-20% effect in
flux at >5 keV, and may result from not accounting for an energy-dependence
in the mirror PSF.
References:
Burrows, D. 1982, Ph.D. Thesis, University of Wisconsin
Mauche, C.W. and Gorenstein, P. 1989, ApJ, 336, 843
Petre, R., Serlemitsos, P.J., Marshall, F.E., Jahoda, K. and Kunieda, H., 1992,
Proc. S.P.I.E., 1546, 72
Serlemitsos, P. J. 1988, Appl. Opt., 27, 1447
Serlemitsos, P.J., Marshall, F.E., Petre, R., Jahoda, K., Boldt, E.A., Holt,
S.S., Mushotzky, R., Swank, J., Szymkowiak, A., Kelley, R., and Loewenstein, M.
1991, in Frontiers of X-ray Astronomy, eds. Y. Tanaka and K. Koyama
(Tokyo: Universal Academy Press), p 221
Seward F. 1992, Legacy, 2, p. 47
Shima, K., Nagai, S., Mikumo, T. and Yasumi, S. 1983, Nuclear Instruments
and Methods in Physics Research, 217, 515
Smale A. P. 1992, Legacy, 2, p. 17
Toor, A. and Seward, F.D. 1974, AJ, 74, 995
Toor, A. and Seward, F.D. 1977, ApJ, 216, 560
Turner, M. J. L., et al. 1989, in Proc. 23rd ESLAB Symp. on Two Topics in
X-Ray Astronomy, eds. J. Hunt and B. Battrick, ESA SP-296, Vol 2,
769
Weaver, K. A., et al. 1995, ApJSuppl, in press
Weaver, K. A. 1993, Ph.D. Thesis, University of Maryland
 Proceed to the next article
Proceed to the next article
 Return to the previous article
Return to the previous article
 Select another article
Select another article
HEASARC Home |
Observatories |
Archive |
Calibration |
Software |
Tools |
Students/Teachers/Public
Last modified: Monday, 19-Jun-2006 11:40:52 EDT
|