NOTICE: This Legacy journal article was published in Volume 1, May 1992, and has not been updated since publication. Please use the search facility above to find regularly-updated information about this topic elsewhere on the HEASARC site.

The Einstein Solid State Spectrometer Calibration

D. J. Christian¹, J. H. Swank²,

A. E. Szymkowiak², and N. E. White³

1: Univ. of Maryland, 2: LHEA, 3: HEASARC

I. The SSS Instrument

The HEAO-2 (Einstein Observatory) Solid State Spectrometer (SSS) consists of a cryogenically cooled lithium-drifted Si(Li) detector at the focus of an X-ray imaging telescope. It subtends a six arc minute-diameter circular aperture and is slightly defocussed so that a point source is blurred to a radius of about one arc minute. The spectral resolution is noise-limited with a 160 eV full width half maximum, which is nearly energy independent over the sensitive energy range of 0.5 to 4.5 keV. Each photon is pulse height analyzed into one of 128 bins, each 45 eV wide. The SSS was operational between November 1978 and October 1979, and observed a wide range of sources including AGN, X-ray binaries, CVs, SNRs, stars, and clusters of galaxies. Detailed descriptions can be found in Holt (1976) and Joyce et al. (1978).

X-ray absorption in the Si(Li) detector generates electron-hole pairs which are collected in a charge sensitive circuit. The energy resolution of the detector depends on the variance in the amount of charge collected and noise in its electronic measurement. The variance in the amount of charge decreases if the detector is cooled to obtain the best energy resolution. The SSS was kept at 100 K by attaching it to a cold plate within a cryostat containing methane and ammonia. A time-dependent build-up of water ice on the detector surface occurred because of cryopumping of ambient outgassing material onto the 100 K detector. It was periodically defrosted by heating the detector to 220 K at the beginning of a series of three day observations. The cryogen was sufficient for 10 months operation, and was exhausted in October 1979, which effectively ended the useful life of the SSS.

II. The Detector Response

To compare the observed SSS spectra with the predictions of a model, the amount of ice on the detector needs to be taken into account, as well as the telescope area, absorption in the detector window, the response of the detector and electronic signal processing. The underlying detector response has many uncertainties, e.g., the telescope area was known from prelaunch calibrations to only 10% (Harnden et al. 1982). During the mission, multiple observations of the Crab Nebula were made to calibrate the response of the detector. The Einstein Observatory observing constraints limited Crab observations to a few weeks in March and September. An Fe⁵⁵ calibration source provided on-board calibration of gain. During the mission, prelaunch estimates for some of the parameters were adjusted on the basis of the initial calibrations (Holt et al. 1979; Becker et al. 1979). The dominant calibration uncertainty is determining the functional form of the ice absorption and its time dependent increase after each defrost. There have been two efforts to understand the SSS response matrix. The first was made in 1979 shortly after launch, and the second in 1990.

A. The 1979 Calibration

Following launch, observations of bright X-ray sources showed the low energy response to be much lower than expected, and indicated that the detector was covered by a layer of water ice. A heater on the cold plate allowed the detector to be defrosted, and an observation immediately after defrost confirmed that water ice was reduced, but that it also built up rapidly again within 12-24 hours. This was attributed to residual water present in multi-layer insulation (MLI) within the cryostat outer shell (the MLI was designed to prolong the lifetime of the cryogens). Molecules hitting the detector surface, the coldest surface in the enclosure, tended to stick and build up a layer of ice. However, as more defrosts were performed, it was found that after each defrost the total amount of ice that returned decreased. There was a small opening in the cryostat to the vacuum of space and after every defrost a fraction of water ice escaped. By the end of the 10 months of operation the ice had been reduced to close to zero.

A predictive model for the accumulation of ice was developed by Holt (1979), which assumed that the detector was partially covered by a uniform thickness of ice and that the fraction of the detector covered increased exponentially after each defrost with an e-folding time of 0.25 day. The model assumed that the averaged ice thickness to be linearly related to the partial covering fraction. This model had one free parameter, the partial covering fraction, which could be adjusted. After each defrost, the partial ice thickness decreased by a small amount. Near the end of the mission, in September 1979, relatively little ice remained. The covering fraction and the total amount of ice were determined for each three-day observing interval using SSS observations of a variety of objects with relatively well-known spectral forms. These were then used to form a predictive model. This introduced systematic uncertainties into any SSS analysis of individual objects, since many of the same objects were used for the calibration and analysis.

The net underlying response of the SSS and telescope were adjusted differentially to best fit the spectrum of an observation of the Crab relatively late in the mission (Szymkowiak 1985). Spectra were fit using this response and the ice model with an adjustable parameter. The effects of absorption by oxygen in the ice are similar at the resolution of the SSS to those of the interstellar absorption for modest column densities. Published uncertainties quoted for column densities of the interstellar medium reflected uncertainty in the scale of the amount of ice.

B. The 1990 Calibration

The 1979 calibration did not produce satisfactory results for observations made early in the mission when the ice covering was high. The behavior of the residuals of fits to the spectra of the Crab and other bright sources suggested systematic errors in the effective area below 1.5 keV. In addition, new results which had a bearing on the calibration became available from the measurements of the Crab spectrum by the Focal Plane Crystal Spectrometer on the Einstein Observatory, which gave a better understanding of the energy-dependent mirror area and the Crab spectrum.

In 1990 two efforts were undertaken, to find a more satisfactory ice model and to reevaluate the underlying instrument response. The re-calibration included the following: 1) a set of cubic splines fit to adjust the telescope area, including adjustment of the mirror's Ni edge based on observations of the FPCS (Schattenburg, private communication and Schattenburg and Canizares 1986), 2) fitting to detector absorption features, including the silicon dead layer, the paralene window, and the gold contact layer, 3) the preflight energy-to-channel conversion of calibration, and 4) differential non-linearity in the analog to digital conversion of the pulse heights (Christian 1992). The last effect resulted from a small (3%) differential non-linearity in the electronics which caused the counts in adjacent PHA channels to fluctuate around a mean value. There is evidence that this effect is present in all the SSS data, but it is only statistically significant when several observations of the Crab are summed, and for other very bright sources. The average of 3 Crab observations (September 17, 18, and October 1), made when the layer of ice present in all of these observations was very thin, was used to initially determine the telescope and detector parameters.

The ice model used in the recalibration is a generalization of the partial covering fraction idea originally proposed by Steve Holt. It assumed the ice to be made up of two thicknesses of granules or snow flakes. The spectral form is

fe^-1^(E)+(1-f)e^-2^(E)

with f the partial covering fraction and ₁ and ₂ the mean optical depths of two ice distributions. This model gave acceptable fits to the Crab data.

There are possible rationales for different thicknesses of ice on parts of the surface of the detector: the thickness at a given time after defrost could have depended on whether deposition started on previously built-up ice or on clean detector surface, or on whether the deposition was over the silicon or deposited gold, or on the location on the detector, e.g. the proximity of edges or defrost heaters.

Calibration of the SSS depends critically on the accuracy of the Crab Nebula spectrum. The photon spectrum used in this calibration was

dN/dE = C E^- exp(-N_H (E))

with =2.1, C=9.5, and N_H = 3.5x10²¹ cm^-2 of interstellar medium and cross-sections according to Morris and McCammon (1983). Toor and Seward (1974) reviewed spectral measurements as of 1974 and deduced that =2.10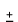0.03, with C=9.7 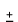1. For historical reasons we used C=9.5, but allowed for adjustment of the norm through an adjustment of the area. Measurements of the column density are well reviewed by Schattenburg and Canizares (1986). Dust scattering can affect the low energy spectrum (Hayakawa 1970) and Toor, Palmieri and Seward (1976) saw possible evidence for it in extended emission. Schattenburg and Canizares included the effects in the analysis of data on the Crab Nebula obtained with the Focal Plane Crystal Spectrometer on the Einstein Observatory. They then obtained N_H =(3.45 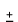0.4) x 10²¹ cm^-2.

Our data could not provide definitive evidence, in the sense of a significantly improved chi-square, for the dust model. Therefore, the effects of dust on the Crab spectrum are included in the combination of effective area and ice model. For these reasons, we treat dust scattering for other sources as a model defined as the ratio of the fractional intensity of the dust correction of the source to the fractional intensity of the dust correction of the Crab. In most cases we have examined, the fits are not very sensitive to dust scattering. In sources for which the column density is large, the scattering out of the beam is large and the spectra are cut off at low energies.

Using the Crab Nebula spectrum discussed above, the calibration procedure proceeded as follows. The detector edge and spline parameters were fit simultaneously to the data of the 3 Crab observations. This solution for the edge and spline parameters then determined the ice parameters for 12 Crab observations taken throughout the mission. These 12 Crab observations were then averaged and a new set of spline and edge parameters determined, taking into account the effect of the ice appropriate to each spectrum included in the average. The ice parameters for the individual observations were then obtained again and the matrix solution iterated until it converged. Figure 1 shows the data, folded model, and residuals of an early Crab observation (March 11, 1979) with high ice thickness, and a late observation (September 18, 1979) with low ice thickness.

Figure 1. Data, folded model, and residuals of a low ice observation (September 18, 1979), and an early high ice Crab observation (March 11, 1979).

The new ice model treats the ice as flakes on the detector with a Poisson number distribution giving a transmission probability of the form

P= exp(-Cl_n(1-exp(-Nc))

where Nc is the average flake column density, Cln is the average number density of 'clumps', n is the clump distribution number, and is the absorption cross section. The model used two clump distributions. The four parameters were determined by fitting early Crab observations with substantial ice thickness to accurately determine the parameters. The four-parameter model was reduced to one parameter, the average number of clumps, Cl₁, by determining relationships between the parameters. Four-parameter fits to the Crab spectra gave a linear relation between the two thicknesses of Th₂=Th₁/26.68, and a linear relation between the number of clumps of different thicknesses, Cl₂=3.02 Cl₁. From these relationships a two-parameter model was fit to the Crab data and a linear relationship was determined between Th₁ and Cl₁ of Th₁=(1.165+1.944 Cl₁). Cl₁, the average number of clumps, was then used to develop a predictive model. The model is shown in figure 2.

Crab observations were only possible in March and September 1979. To obtain further constraints on the ice model earlier than March and in June 1979, several sources with simple spectra were used. Observations of Cyg X-2, LMC X-3, and X 0918-549 were used to constrain the model in the first 60 days. During this time there was a long period, December 11, 1978 to January 9, 1979, when the SSS went without a defrost. Over this long interval the total ice that accumulated was no more than after a short defrost interval (~10 days), indicating a fixed volume of water ice, rather than a continuous outgassing. Observations of 3C273 near Day 540 (June 24, 1979) of the mission were used to constrain the model between the two Crab observation epochs.

The ice which was evaporated from the detector during each defrost ended up in one of three places: some stuck to the MLI in the cryostat, a small fraction was lost, and the remainder (the vast majority) remained as vapor-ice. After each defrost, the modelling required that the ice return in two components. First, the vapor-ice returns with an e-folding time of 0.25 day (as in the original calibration). Second, the ice on the MLI returns on a much longer timescale with an e-folding of order 10 days.

This modelling allows the ice to be predicted with known uncertainties after January 1979. This model has been implemented into VIMAT. When running VIMAT it produces a response for the epoch of the observation (see Drake, 1992). Ice uncertainties at different epochs of the mission are given below in Table 1. Before this, during the first 60 days of the SSS operations, there was a long interval where no defrost was made and those that were made were of variable duration, both of which add unpredictable complications to the model. Figure 2, shown below, gives the ice parameter as a function of time during the mission. The uncertainties in the predictive ice model are given in Table 1. Observations after the first set of Crab observations in March 1979 have the best predictive ice model, while observations before this date have the largest uncertainties and predictions made should be used with caution. In these cases, the user should fit using the ice model (in XSPEC this is the model SSS_ice). When running VIMAT, a zero ice response matrix is automatically generated. Note that users cannot do simultaneous MPC/SSS fits when determining the ice.

Figure 2. The ice parameter as a function of time during the mission. Error bars are plotted for Crab and other observations used to constrain the model.

	                                Table 1

	Observations 	      Ice parameter         Comment

	Dec. 1 - 4, 1978	 --------    Ice is not predictable.
	Dec. 4 - 16, 1978 	 +/- 1.5     Dec. 4 observation occurs after a 
                                             long defrost which causes the major
                                             uncertainty. Ice parameters 
                                             determined with Cyg X-2 and 3C273.
	Jan. 9 - Mar. 10, 1979 	 +/- 0.6     Interval follows 30 day run in 
                                             which no defrosts were performed. 
                                             Ice determined by average of LMC 
                                             X-1 and LMC X-2 spectra.
	Mar. 10 - Mar. 29, 1979  +/- 0.1     Uses Crab observations. Ice is well
                                             determined. 
        Mar. 29 - Sept. 2, 1979  +/- 0.4     Interval between the two Crab
                                             observation runs.  3C273 spectra 
                                             are used from June 24, 1979.
	Sept. 2 - Oct. 7, 1979	 +/- 0.1     Uses Crab observations. Ice is well
                                             determined. 

III. The Instrument Background

The total background due to all non-source contributions is 0.28 ct/s above 0.5 keV and 0.19 ct/s above 1 keV. Background is not measured simultaneously, and must be estimated from data accumulated over source-free exposures. Subsequently the background was modeled from 10,000 seconds of blank sky observations. The background consists of two separate components; one related to cosmic ray and particle events and almost independent of energy, and a second, more variable, component above ~3 keV. The separate background components are shown in Figure 3. The total background for a particular observation is determined from the standard background model, and by fitting to determine the fraction of the second component. Within the spectral fitting package, XSPEC, a "recornorm" command is used to fit the amount of the second background component to minimize the 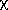² statistic. The renormalization parameter should be between 0.0 and 1.2. If it is outside this range, the spectral model is probably not acceptable.

Figure 3. The SSS background showing the two components as a function of arbitrary channel number. Channel 26 corresponds to 1.03 keV.

References

Becker, R. H., Holt, S. S., Smith, B. W., White, N. E., Boldt, E. A., Mushotzky, R. F., and Serlemitsos, P. J., 1979, Ap.J., 234, L73.

Christian, D. J. 1992, Univ. of Maryland Ph. D. Thesis.

Harnden, F.R., Fabricant, D.G., Harris, D.E., and Schwarz, J. 1982, "Data Analysis System for the Einstein Observatory" p. 274.

Hayakawa, S. 1970, Prog. of Theoretical Physics, 43, 1224.

Holt, S. S. 1976, Space Sci. Instr., 2, 205.

Holt, S. S., White, N. E., Becker, R. H., Boldt, E. A., Mushotzky, R.F., Serlemitsos, P., J., and Smith, B. W. 1979, ApJLet, 234, L65.

Joyce, R. M., Becker, R. H., Birsa, F. B., Holt, S. S., and Noordzy, M. P. 1978, IEEE Trans. Nuc. Sci. NS-25, No 1, 453.

Morris, R., and McCammon, D. 1983, Ap.J., 270, 119.

Schattenburg, M.L., and Canizares, C.R. 1986, Ap.J., 301, 759.

Szymkowiak, A. E. 1985, Univ. of Maryland Ph.D. Thesis.

Toor, A. and Seward, F.D. 1974, Astron.J., 79, 995.

Toor, A., Palmieri, T. M., and Seward, F. D. 1976, Ap.J., 207, 96.

Proceed to the next article

Return to the previous article

Select another article