It should be noted that this is not intended to be the definitive write-up of
the PSPC p.s.f. Rather, the aim of the memo is to distribute the
currently available information to ROSAT PIs in a timely fashion. The
author list does not reflect the input of all the people involved with the
PANTER data. It is expected that a full write-up will appear at a later
date.
The Ellipsoidal blur due to residual attitude motion
These are individually discussed in more detail below. Specifically the
on-axis p.s.f. is described in detail, comparing the form derived from
an analysis of ground calibration data with that obtained in orbit. The
off-axis p.s.f. will be discussed in more detail in a future OGIP
calibration memo.
Throughout,
is the off-axis angle (in arcmin) from
the center of the PSPC
field of view,
r is the radius (in arcmin) from the p.s.f. centroid,
PSF(E,r) is the p.s.f. (in normalized cts
area-1),
and E is the photon energy (in keV).
1.1 The XMA Scattering Profile
Microroughness of the reflecting mirror surfaces leads to non-specular
reflection of X-rays, i.e., scattering. Theoretically, assuming the
grazing angle remains constant, the scattering fraction should increase as
E2. Due to the laws of diffraction, the shape parameters
should be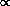 
E-1.
The importance of scattering by the ROSAT XMA is small compared to
previously available X-ray mirrors, offering the ability to perform high
contrast imaging. The form of the scattering is a complex function of energy,
grazing angle and the scale size of the mirror surface roughness. The
combination of these effects can be modelled as a Lorentzian which breaks to a
power law at high radii.
1.2 The Off-axis Blur of the XMA
The off-axis p.s.f. of grazing incidence optics is rather complicated.
A convenient measure of the image spread is the so-called RMS blur radius,
defined as the radius within which 68% of the photons fall, i.e., the
Gaussian sigma of the distribution of photons for a given off-axis angle. The
expected ROSAT XMA rms blur circle radius, rblur, increases
rapidly with off axis angle. The off-axis effects will be treated in a
subsequent p.s.f. memo.
1.3 The Intrinsic Resolution of the Counter
Due to the inherent statistics of the primary electron generation, the
intrinsic spatial resolution of the ROSAT PSPC is expected to be a
Gaussian. Theoretically its width is 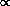E -1/2
and independent of .
1.4 Focus and Penetration Effects
The design distance between the XMA and PSPC (the window of which is flat) is
such that photons of ~1 keV on-axis source are brought to a focus (along a
surface of a cone of half-angle 8.5° ) at an optimum depth within the PSPC
drift region such that the Gaussian spatial distribution of pulses on the
cathode wires is minimized. Consequently the image of a point source is
sharpest at 1 keV.
1.5 Ghost Images
The position of an event in the PSPC is determined from the amplitudes of
signals on the two cathode grids. The specific algorithm uses the two highest
signals from each cathode grid (the cathode grids are divided into something
like 22 segments with separate amplifiers). For events with large pulse-height
amplitudes, this works very well since the strength of the signals on the
cathode segments is related to the strength of the signal on the anode.
However, for small pulse-height amplitudes, occasionally only one cathode
segment of a grid will have a signal above the lower discriminator. This still
gives a well specified, but incorrect, position. If two segments of one grid
have signals but only one of the segments from the other grid has a signal,
then the determined position will lie along a line. If only one segment from
each grid has a signal, then the determined position will lie at a point. This
structure is very apparent when looking at an image of events in detector
coordinates with pulse heights less than channel 15 (~ 0.15 keV). There is a
cross-work pattern of lines with bright spots at the intersections. There are
secondary bright spots in the centers between the lines since the probability
is greater there to get signals on four cathodes.
1.6 Ellipsoidal blur due to residual attitude motion
Generally, SASS processing allows only data of good attitude solution to be
included in the "Good-Time Intervals" (GTIs). Only data with attitude
solutions better than ~2 arcsec are included in the GTIs for sequences
processed by SASS after 1991 Dec (earlier processing had a looser constraint on
the attitude solution, sometimes resulting in a noticeable asymmetric blurring
of the image).
2 Ground Calibration Data
The detailed p.s.f. parameters and their associated E dependences
have been determined for PSPC-A & PSPC-C using 4 monochromatic energies
(0.28, 0.93, 1.49 & 1.70 keV) at the PANTER test facility in Garching.
Currently, results for three of the components of the p.s.f. have been
determined -- namely the PSPC intrinsic resolution, focus and penetration
effects and the effects due to mirror scattering. In principle the resultant
three components should be folded with each other, however, they are
sufficiently well separated in the r (spatial) domain that MPE considers
a simple addition accurate enough.
2.1 The XMA Scattering Profile
The analytical form derived for the fraction of photons within this component
as a function of energy is given by:
Fscatt = 0.059 E+1.43 (1)
It can be seen from Figure 1 that even at high energies Fscatt
is small
compared to the other components. The model and the PANTER data from which eqn
1 was derived are also shown in Figure 2. The increase in Fscatt with
E is slower than the E2 powerlaw expected due to the
detailed structure (micro-roughness) of the mirror surface.
The PANTER tests confirmed that this component was well approximated by a
Lorentzian, as expected (Section 1.1), steepening to a powerlaw at large
r, i.e.,
PSFscatt(E,r) = ![A_scatt (E) / [1 + (2r/r_scatt(E))^2]](pspc2-3.gif)
for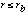 
= PSF(E,rb) (r/rb)-
for 
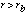(2)
where
rb(E) = 861.9/60 E-1 arcmin (3)
and
= 2.119 + 0.212E (4)
The width of the Lorentzian, rscatt(E), as a function of energy
was found to be:
rscatt(E) = 79.9/60 E-1 arcmin (5)
and is plotted in Figure 3. The two parameters governing the shape of
PSFscatt(E) (i.e., rb and rscatt) were constrained to
be proportional to E-1 (see section 1.1) during the
analytical fitting to the PANTER data.
The normalization of the Lorentzian, Ascatt,is given by
Ascatt = Fscatt(E) /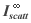 
normalized cts arcmin-2 (6)
where
= 
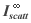(rscatt/2)2 [ln (1 + (2/rscatt)2 rb2) + 2 rb2 ((rscatt/2)2 + rb2)-1( - 2)-1] (7)
is the renormalization factor such that[1]
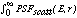2r dr = Fscatt(E) (8)
Ascatt is plotted as a function of E in Figure 4.
The fraction of incident photons scattered outside a radius, rcell, is
shown as a function of energy for various rcell in Figure 5. It should
noted that at 1 keV, ~ 6% of incident photons will be scattered outside
rcell = 100 arcsec, and ~ 5% outside rcell = 10 arcmin.
To summarize:
At low energies, the strength of this component to the p.s.f. is very
small, and its width very large, making it difficult to distinguish this
component from the background and/or slow variations in the efficiency of the
PSPC. As one moves to higher energies (
0.5 keV), the strength of
the component increases and the width decreases, increasing the importance of
this component to the total p.s.f. (see Figure 6).
At energies for which the analytical parameterization of the PANTER data is
valid (i.e.,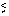 
2 keV), the steepening from a Lorentzian to a
powerlaw form occurs at radii, rb 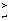10 arcmin. Since the break
is relatively gentle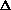 
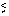0.4), this is unlikely to
be detectable in most datasets.
2.2 The Intrinsic Resolution of the PSPC
All photons not in the other 2 components are assumed to be in this component.
Thus the fraction of photons within this component as a function of energy is
given by:
Fint = 1 - Fscatt - Fexp (9)
As discussed further in Section 2.3, eqn 9 is only valid for E
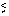2.0 keV as above this energy the derived analytical expression for
Fexp implies Fexp > 1 and hence
Fint < 0.
The PANTER tests confirmed that this component was well approximated by a
Gaussian, as expected from the statistics of the primary electron generation
process (Section 1.3); i.e.,
PSFint(E,r) = Aint(E) exp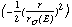
normalized cts arcmin-2 (10)
The derived analytical form for the width of the Gaussian,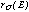 
,
as a function of energy is given by:
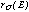= 1/60 ( 108.7 E-0.888 + 1.121E+6)1/2 arcmin (11)
and is plotted in Figure 3. The model and the PANTER data from which eqn 11
was derived are also shown in Figure 2. It can be seen that
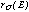decreases and then increases with increasing
E within the PSPC band, with a minimum at
E 
1.5 keV. It should be noted that at low energies, the analytical function
decreases slightly more slowly with E than the PSF(E)
E2 expected (Section 1.3). For
all E within the PSPC energy band,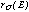
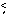0.5 arcmin
The normalization, Aint(E), is given by
Aint(E) = Fint(E) / 2(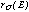)2) normalized cts arcmin-2 (12)
where the denominator is the renormalization factor such that the integral of
PSFint(E,r) r dr over the range 0
r
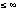equals
Fint(E). Aint is shown as a
function of E in Figure 4.
2.3 Focus and photon penetration effects
The analytical form derived for the fraction of photons within this component
as a function of energy is given by:
log10Fexp(E) = -1.618 + 0.507E + 0.148E2 (13)
Thus the importance of this component rises relatively quickly with E
(Figure 1). The model and the PANTER data from which eqn 13 was derived are
also shown in Figure 2. It should be noted that for E
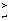2.0 keV, eqn 13 implies Fexp(E) > 1.
This is clearly a physically meaningless result, and gives an upper limit on the applicability of the
analytical functional forms derived from the PANTER measurements. (The highest
photon energy at which the PANTER measurements were carried out was 1.70
keV.)
The combined contribution of focussing and the finite penetration of photons
into the counter on the p.s.f. can be is modelled as an exponential
function:
PSFexp(E,r) = Aexp(E) exp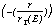 
normalized cts arcmin-2 (14)
The e-folding angle,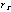 
, was found to be given by
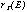= 1/60 (50.61 E-1.472 + 6.80 E+5.62)1/2 arcmin (15)
and is plotted in Figure 3 (see also Figure 2). It can be seen that
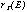is a minimum at E (~,-) 1.1 keV reflecting the fact
that the separation between the XMA and PSPC is such that 1 keV photons are
brought to a focus at an optimum depth within the counter.
The normalization, Aexp(E), is given by
Aexp(E) = Fexp(E)/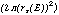
normalized cts arcmin-2 (16)
and as for the other components has been normalized such that the integral of
PSFexp(E,r) r dr over the
range
0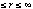 
equals Fexp(E). Aexp(E) is
plotted as a function of E in Figure 4.
To summarize:
The fraction of the photons within this component increases with E
(Figure 1); the normalization of the resultant exponential component to the
p.s.f. increases with E, then flattens off at ~ 1 keV; whilst
the e-folding angle (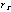) decreases with E for energies
below ~ 1 keV, then increases with E at higher energies.
2.4 The Predicted Composite p.s.f.
The predicted composite p.s.f., PSFtot, for the ROSAT XMA
+ PSPC combination at a given energy is given by the addition of the components
given above (i.e., PSFscatt + PSFint + PSFexp). Examples
of PSFtot are shown in in Figure 6 (solid lines) at several energies,
along with curves showing the three individual components. In Figure 7 are
shown the corresponding curves of the predicted encircled fraction as a
function of radius. For convenience, the radii encircling 50, 90, 95 & 98%
of the photons are also listed in Table 1 and plotted in Figure 8. It can be
seen that above ~ 1 keV, it is predicted that a substantial fraction (~ 5%) of
photons will be scattered by the XMA outside a radius
10 arcmin
(see also Figure 5).
Table 1: Encircled Fraction
Energy Radius (arcmin)
(keV) 50% 90% 95% 98%
------------------------------------
0.188 0.44 0.81 0.94 1.14
0.284 0.36 0.68 0.79 0.99
0.5 0.29 0.54 0.65 2.20
1.0 0.22 0.45 1.55 >10
1.7 0.28 1.36 8.79 >10
In Figure 9, the predicted p.s.f. is compared directly with the PANTER
data from which it was derived. It can be seen from the residuals that the
fits are generally satisfactory, particularly at radii
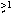arcmin.
It should be emphasized that the above analytical parameterizations are only
valid over the energy range 0.15 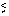E
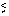2.0 keV (i.e.,
channels 15-200).
3 The In-flight Data
3.1 Datasets & Extraction
The above Ground Calibration results have been tested against the in-flight
datasets listed in Table 2. The letter in parentheses after the ROR number
indicates which PSPC was used to obtain the data (PSPC-C was in use prior to
its destruction during the sun pointing on 1990 Jan 25). While ideally we would
have preferred to use bright calibration sources, many of the sources observed
in the first calibration phase are unsuitable for this study. AR LAC was never
observed on-axis with the PSPC (in the first calibration datasets) and many of
the other calibration targets are extended, often due to the presence of a dust
halo. Some satellite maintenance observations which have been made more
recently will be used to check these results, but in the meantime we have
tested against several point source datasets. Two of the datasets were from the
long pointing phase and hence provide excellent signal-to-noise. In any cases
where there was some evidence for an extended feature in the point source, or
where there were other sources close to the on-axis point source, suitable
exclusion regions were set for the profile extraction. Data attitude solutions
were checked, and any data with attitude error greater than 2 arcseconds was
excluded from the analysis.
Table 2: On-axis In-Flight Datasets
No. ROR Object Class Exp (ksec) Comment
-------------------------------------------------------------------
1 rp150071 (C) NGC5548 Seyfert 1 18.86 PV
2 rp700055 (B) NGC3998 LINER 22.85 AO1
3 rp700057 (B) Pictor A LINER 4.46 AO1
4 rp700105 (B) Mkn509 Seyfert 1 1.77 AO1
5 rp700104 (B) ESO141 Seyfert 1 5.02 AO1
Radial profiles were extracted using PROS in the five energy bands listed in
Table 3. Five was considered optimum for energy resolution with good signal to
noise in each band. Typically several thousand counts per source per bandpass
were obtained for comparison with the predicted p.s.f.
Table 3: The Energy Bands Used
Name Energy (keV) PI Channels
min max min max
B 0.10 0.188 9 18
C 0.188 0.284 19 29
R1 0.284 0.5 30 50
R2 0.5 1.0 51 101
R3 1.0 2.48 102 256
The lowest 8 channels were rejected to exclude problems due to the variable
lower limit discriminator for valid events, due to the variable instrument gain
which is folded into these data.
The following specifications were applied to the data:
The counts profiles were rebinned such that each spatial bin contained at
least 20 photons.
Table 4: Results
No. ROR Bkgd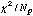 
(ct arcmin-2)
B-band
1 rp150071 (C) 1.4 x 10^-3 282/27
2 rp700055 (B) 8.6 x 10^-3 832/39
3 rp700057 (B) 7.2 x 10^-3 192/9
4 rp700105 (B) 1.5 x 10^-3 41/14
5 rp700104 (B) 3.3 x 10^-3 57/14
C-band
1 rp150071 (C) 9.2 x 10^-4 68/22
2 rp700055 (B) 5.1 x 10^-3 295/36
3 rp700057 (B) 4.0 x 10^-4 62/13
4 rp700105 (B) 8.6 x 10^-4 65/15
5 rp700104 (B) 1.5 x 10^-3 29/17
R1-band
1 rp150071 (C) 7.6 x 10^-4 56/19
2 rp700055 (B) 3.5 x 10^-3 143/26
3 rp700057 (B) 4.0 x 10^-3 27/12
4 rp700105 (B) 7.5 x 10^-4 18/12
5 rp700104 (B) 1.2 x 10^-3 53/16
R2-band
1 rp150071 (C) 5.5 x 10^-4 15/17
2 rp700055 (B) 1.0 x 10^-3 66/24
3 rp700057 (B) 1.8 x 10^-3 47/16
4 rp700105 (B) 2.5 x 10^-4 17/12
5 rp700104 (B) 6.8 x 10^-4 39/20
R3-band
1 rp150071 (C) 5.3 x 10^-4 56/22
2 rp700055 (B) 6.3 x 10^-4 31/22
3 rp700057 (B) 9.4 x 10^-4 34/15
4 rp700105 (B) 1.9 x 10^-4 24/14
5 rp700104 (B) 4.0 x 10^-4 37/19
3.2 Theoretical Curves
The detailed p.s.f. parameters and their energy dependence have been
determined using the PANTER telescope calibration data of both PSPC-A and
PSPC-C at the monochromatic energies 0.28, 0.93, 1.49 and 1.70 keV. At lower
pulseheights than channel 15 (0.15 keV) additional 'ghost images' appear in
the PSPC, as described in the previous section, for which no analytical fit is
possible. Fits to the B band data are shown to illustrate this point. We will
return to this point in the summary.
As the in-flight data are affected by more uncertainties than the ground data
(aspect corrections, background subtraction, gain correction etc.) it
was not possible to allow profile fitting with the parameters of the Gaussian +
exponential + Lorentzian components to be free. Instead we calculated the
p.s.f. for every source in each bandpass.
First, a spectrum was extracted for each source, in a circle of size several
arcminutes radius (exact region mask used depended on the particular field) to
ensure that essentially all of the sources counts were collected. Next, a
p.s.f. was calculated for each energy channel. A predicted p.s.f.
template was calculated for each dataset using the source spectrum to determine
the photon weighting to be applied to the p.s.f. component in each
energy channel. Thus for each band and spectrum a combined p.s.f. was
produced, including a constant term for the background component from Table
4.
These predicted templates were overlaid on the appropriate datasets as
illustrated in Figure 10. As the normalization of the model was also
calculated (using the equations in Sections 2.1, 2.2 and 2.3), NO
FITTING was performed. The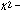 
statistic for each dataset
and band is listed in Table 4. It can be seen that, except in the case of the
B band, the model generally gives a good description of the p.s.f. Some
slight discrepancies are observed, as can be seen from Figure 10 (particularly
the case for NGC 3998). As NGC 3998 is a nearby galaxy, part (or all) the
deviation observed in this source may be an indication of genuine extended
X-ray emission. This and the fact that no systematic deviations are observed
across the other datasets tested leads us to conclude that the p.s.f.
model should not be modified based on the NGC 3998 deviations alone.
Comparison of more point source datasets should be made before we can determine
whether effects such as this should be modelled.
4 Conclusions
The MPE model for the PSPC p.s.f. is good for energies between 0.15 and
2.0 keV. Generally the predicted shape agrees well with the data, with no
obvious systematics in any band except the B-band. Thus, within the
statistical limits of these datasets, we conclude the model is a satisfactory
description of the PSPC p.s.f. More bright source datasets are expected
to become available to the ROSAT GOF within the next few months. These
may provide a more stringent test of the model, and any discrepancies found
will be noted in future OGIP Calibration Memos.
The MPE model does not satisfactorily predict the observed B-band p.s.f.
Whilst Figure 10a illustrates the effect of Ghost imaging at low energies, this
effect is not (yet) quantifiable. Thus at present, it is recommended that
users extract data products within a large enough region such that most the
B-band counts are included and a negligible correction is required (see Figure
7 and 8).
Acknowledgements
We thank the many people at MPE involved in the determination &
interpretation of the PANTER data, Dave Davis (GSFC) for his help extracting
the data and Gail Reichert (GSFC) for supplying some test datasets from her own
AO-1 observations.
Figure 1 The fraction of photons in the 3 major components of the
ROSAT PSPC on-axis p.s.f. verses photon energy. The functional
forms were determined from analytical fits to Ground Calibration measurements
on PSPC-A & PSPC-C in the PANTER facility. The fraction of photons within
the component due to (1) the intrinsic spatial resolution (a Gaussian) is shown
dashed (Fint); (2) the chromatic aberration and finite photon
penetration (an exponential) is shown as the dot-dash curve (Fexp); and
(3) the XMA mirror scattering (a Lorentzian) is shown dotted (Fscatt).
For reference, the 4 energies at which the PANTER measurements were made are
also indicated. It can be seen that the analytical forms break down above ~2
keV, when Fexp > 1 and hence Fint < 0 (see text).
Figure 2 The PANTER data and the derived analytical functions
describing various components of the on-axis p.s.f. of the ROSAT
XMA + PSPC combination. Top left panel: the width,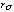 
, of the
Gaussian describing the intrinsic spatial resolution of the PSPC (eqn 11);
Bottom left: the fraction of photons, Fexp, within the
exponential
component due to the combined effects of chromatic aberration and the finite
penetration depth of photons (eqn 13) Top right: the e-folding angle,
rscatt, of the exponential describing the shape of the
component of the
p.s.f. due to these effects (eqn 15); Bottom right: the fraction of
photons, Fscatt, within the Lorentzian component due to
scattering by
the XMA (eqn 1).
(Source: Hasinger Notes, 1992 Feb 17).
Figure 3 The energy dependence of the parameters governing the shape of
the 3 major components of the ROSAT PSPC on-axis p.s.f., as
determined from analytical fits to Ground Calibration measurements on PSPC-A
& PSPC-C in the PANTER facility. The curves are: (dashed) the width of the
Gaussian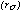 
component due to
intrinsic spatial resolution of
the PSPC; (dot-dashed) the e-folding radius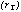 
of the
exponential function describing the combined effects of chromatic aberration
and the finite penetration of photons into the counter; and (dotted) the width
of the Lorentzian rscatt component due to scattering by the
ROSAT XMA. For reference, the 4 energies at which the PANTER
measurements were made are also indicated.
Figure 4 The normalizations of the 3 components of the ROSAT
PSPC p.s.f. as a function of energy. The curves are the normalizations:
(dashed) Aint, of the Gaussian component arising from the
intrinsic
spatial resolution of the PSPC (eqn 12); (dot-dashed) Aexp, of
the
exponential function describing the combined effects of chromatic aberration
and the finite penetration of photons into the counter (eqn 16); and (dotted)
Ascatt, of the Lorentzian due to scattering by the XMA (eqn 6).
For
reference, the 4 energies at which the PANTER measurements were made are also
indicated.
Figure 5 The predicted fraction of photons, as a function of energy,
scattered outside radii rcell = 10, 100 & 600 arcsec for an
on-axis
source.
Figure 6a The predicted on-axis p.s.f. for the ROSAT
PSPC for various energies derived from the analytical fitting of PANTER
calibration data. The Gaussian, exponential and Lorentzian components are
shown dashed, dot-dashed and dotted respectively, with the solid curve giving
the composite. Note that in order to demonstrate the structure of the
scattered component, the r-axis has been extended beyond the fov
of the PSPC.
Figure 6b Close-up of inner region of the predicted (composite)
ROSAT PSPC p.s.f. for various energies.
Figure 7 The predicted fraction of encircled photons for the
ROSAT PSPC as a function of radius for various energies.
Figure 8 The radii encircling 50, 90 & 95% of the photons for the
ROSAT XMA + PSPC, as predicted from the the analytical expressions
derived from the PANTER p.s.f. calibration measurements.
Figure 9 The predicted p.s.f. (solid line) compared to the
PANTER data from which it was derived.
(Source: Hasinger Notes, 1992 Feb 17).
Figure 10a The observed p.s.f. of the ROSAT PSPC in the
B-band (0.1--0.188 keV) compared to that predicted from the ground calibration
data. The figures are numbered as listed in Table 2. The large discrepancies,
due to the effects of Ghost images in the band (see Section 1.5) are clearly
apparent.
Figure 10b As for Figure 10a, but for the C-band (0.188--0.284 keV).
Figure 10c As for Figure 10a, but for the R1-band (0.284--0.5 keV).
Figure 10d As for Figure 10a, but for the R2-band (0.5--1.0 keV).
Figure 10e As for Figure 10a, but for the R3-band (1.0--2.48 keV).
Note, the predicted p.s.f. for this band were calculated using the
spectral data below 2.0 keV only.
Proceed to the next article
Return to the previous article
Select another article
HEASARC Home |
Observatories |
Archive |
Calibration |
Software |
Tools |
Students/Teachers/Public
Last modified: Monday, 19-Jun-2006 11:40:52 EDT
