NOTICE:
This Legacy journal article was published in Volume 4, February 1994, and has not been
updated since publication. Please use the search facility above to find regularly-updated information about
this topic elsewhere on the HEASARC site.
|
ROSAT PSPC
Off-Axis Point Spread Function
Gunther Hasinger (MPE), Gunter Boese (MPE),Peter Predehl (MPE),
T. Jane Turner (NASA/GSFC), Rehana Yusaf (NASA/GSFC), Ian M. George (NASA/GSFC), & Gail Rohrbach (NASA/GSFC)
MPE/OGIP Calibration Memo CAL/ROS/93-015 Version: 1993 Sept 18
Summary
This article details the extension of the description of the point spread
function of the ROSAT PSPC to include off-axis effects. We present the off-axis
psf algorithm and compare the model to in-flight data We discuss the limitations
of this parameterization with respect to data analysis.
1 The Data and Model
As detailed in CAL/ROS/92-001 (Hasinger et al. 1992, hereafter H92), the point
spread function (psf) of the ROSAT X-ray mirror assembly (XMA) + PSPC is a
convolution of 5 components:
1. The XMA scattering profile
2. The off-axis blur of the XMA
3. The intrinsic spatial resolution of the PSPC
4. Focus and detector penetration effects
5. A widening of the PSPC resolution due to the existence of 'Ghost images'
(for PHA channels
< 20 only)
There is also some residual ellipsoidal blur due to residual attitude motion,
but for the PSPC, this component is usually negligible compared to the other
effects (see H92 for more details). The XMA scattering profile, the intrinsic
spatial resolution of the PSPC, and focus and detector penetration effects have
already been described in H92 and Hasinger et al. 1993. The psf was parameterized
for on-axis observations from PANTER ground calibration measurements. In H92 it
was shown that the derived analytical functions satisfactorily described 5
moderate signal-to-noise datasets in all but the softest band where 'Ghost
Imaging' was already known to be a problem. Here we extend the treatment to
include a parameterization of the change in shape of the psf with off-axis
angle.
Examination of a bright point source observed off-axis reveals an asymmetry in the distribution of source counts that becomes
easily noticeable once the source is observed outside of the central ring of the PSPC (i.e. > 20 arcmin off-axis). The
asymmetry is produced because for off-axis irradiation half of the mirror sees a different grazing angle to the other. The two
relatively sharp outer boundaries of the blur area, which have different radii of curvature, are produced by the front and
rear aperture planes of the mirrors, respectively. The hole in the psf is due to the central hole in the mirror aperture (the
mirror consists of three shells) defocused at large angles as the detector is flat but the focal plane is curved. The radial
struts also interfere with the photon distribution as they shadow part of the detector. This combination produces the
diffraction-like radial pattern seen on bright sources observed at large offset angles. Figure 1 shows the image of a source
at an offset angle of 40 arcmin for a) inflight data and b) PANTER calibration data, where the center of the detector is
towards the upper left hand side of the image in each case.
While early attempts to parameterize the change in shape of the psf
concentrated on the ground
calibration data taken at the PANTER facility, a comparison of those data with
in-flight data
showed significant differences. These differences are due to the finite source
distance in the
PANTER facility, which results in a beam divergence of about 10 arcmin. The
consequence of this
is that the PANTFR data have the hole on the inner side of the peak of counts
for off-axis sources,
while the in-flight data show the opposite effect (compare figures 1a and 1b).
In addition, the
PANTER image shows greater interference between the psf and the PSPC wire grid
(effects which
are reduced by the wobble of in-flight observations). As a consequence of these
differences,
in-flight data collected from a variety of bright serendipitous sources
detected in pointed
observations were finally used to parameterize the off-axis dependence of the
psf, while the
components which are independent of off-axis angle were carried over from the
higher-quality
on-axis data.
The off-axis blur of the telescope, although highly structured and asymmetric,
has been modeled
by a simple Gaussian for comparison to a azimuthally integrated profile. This
Gaussian term for the
off-axis blur is added in quadrature to the Gaussian term describing the
intrinsic PSPC resolution.
Since the model approximates the behavior of the detector by the addition of
Gaussian, exponential
and Lorentzian terms, instead of a mathematically correct convolution of terms,
then we have to
adjust the contribution of the other terms relative to the on-axis case, to
allow for the off-axis
behavior of the Gaussian term. The new term for the exponential fraction
describes the relative
diminishing of this term with increasing offset angle, due to the increase of
the Gaussian term.
2 The Off-Axis Parameterization
Throughout,
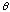 is the off-axis angle (in arcmin) from the center of the PSPC field of view,
is the off-axis angle (in arcmin) from the center of the PSPC field of view,
r is the radius (in arcmin) from the PSF centroid,
PSF(E,r,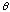 )
is the psf (in normalized cts arcmin2), )
is the psf (in normalized cts arcmin2),
and E is the photon energy (in keV).
2.1 The mirror scattering term
The analytical form derived for the fraction of photons within this component
as a function of
energy is given by:
Fscatt = 0.075 E+1.43 (1)
The increase in Fscatt
with E is slower than the E2
powerlaw expected due to the detailed structure
(micro-roughness) of the mirror surface.
As in the on-axis case, this steepens to a powerlaw at large r, i.e.
PSFscatt(E,r) = ![A_scatt (E) / [1 + (2r/r_scatt(E))^2]](pspc2-3.gif) for for 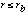 = PSF(E,rb) (r/rb)-
= PSF(E,rb) (r/rb)- for for 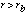 (2) (2)
where
rb(E) = 861.9/60 E-1 arcmin (3)
and
 = 2.119 + 0.212E (4) = 2.119 + 0.212E (4)
The width of the Lorentzian, rscatt,
as a function of energy was found to be:
rscatt(E) = 79.9/60 E-1 arcmin (5)
The normalization of the Lorentzian, Ascatt, is given by
Ascatt = Fscatt(E) / 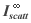 normalized cts arcmin-2 (6) normalized cts arcmin-2 (6)
where
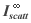 = =  (rscatt/2)2 [ln (1 + (2/rscatt)2 rb2) + 2 rb2 ((rscatt/2)2 + rb2)-1 (rscatt/2)2 [ln (1 + (2/rscatt)2 rb2) + 2 rb2 ((rscatt/2)2 + rb2)-1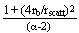 ] (7) ] (7)
is the renormalization factor such that [1]
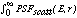 2 2 r dr = Fscatt(E) (8) r dr = Fscatt(E) (8)
2.2 The exponential focus and penetration depth term
The analytical form derived for the fraction of photons within this component
as a function of
energy is given by whichever is the smaller of the following two terms:
Fexp(E, ) = 10-1.635+0.639E+0.052E2e-0.5( ) = 10-1.635+0.639E+0.052E2e-0.5( /12)2 (9) /12)2 (9)
OR
Fexp(E, ) = 1.0 - Fscatt (10) ) = 1.0 - Fscatt (10)
Equation 10 is necessary to avoid the "exponential artifact" of H92 which made
the psf parameterization invalid above 2 keV.
The combined contribution of focusing and the finite penetration of photons
into the counter on the psf can still be modeled as an exponential function
where r is the radial distance from the centroid position of the radial
profile, in arcmin.
PSFexp(E,r) = Aexp(E) exp[-r/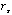 (E)] normalized cts arcmin-2 (11) (E)] normalized cts arcmin-2 (11)
The e-folding angle, 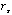 , was found to be the same as for the on-axis case , was found to be the same as for the on-axis case
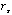 (E) = 1/60 (50.61E-1.472+6.80E+5.62)1/2 arcmin (12) (E) = 1/60 (50.61E-1.472+6.80E+5.62)1/2 arcmin (12)
The normalization, Aexp(E), is given by
Aexp(E) = Fexp(E)/(2 ( (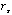 (E))2) normalized cts arcmin2 (13) (E))2) normalized cts arcmin2 (13)
and as for the other components has been normalized such that the integral of
PSFexp(E,r) 2  r dr over the range r dr over the range 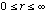 equals Fexp(E).
equals Fexp(E).
2.3 The Gaussian intrinsic resolution and mirror blur term
All photons not in the other 2 components are assumed to be in this
component. Thus the fraction of photons within this component as a function of energy is given by:
Fint = 1 - Fscatt - Fexp (14)
Note that this becomes zero above 2 keV from equation 10.
PSFint(E,r) = Aint(E) exp(-1/2 (r/r (E))2) normalized cts arcmin-2 (15) (E))2) normalized cts arcmin-2 (15)
The derived analytical form for the width of the detector Gaussian,
G (E, (E, ),
as a function of energy is given by: ),
as a function of energy is given by:
r (E) = 1/60 (108.7E-0.888 + 1.121E+6)1/2 arcmin (16) (E) = 1/60 (108.7E-0.888 + 1.121E+6)1/2 arcmin (16)
The analytical form for the Gaussian mirror blur is
m ( ( ) = 1/60 (0.219 ) = 1/60 (0.219 2.848)1/2 arcmin (17) 2.848)1/2 arcmin (17)
These two Gaussian widths are combined as follows:
G (E, (E, ) = r ) = r 2 + m 2 + m 2)1/2 (18) 2)1/2 (18)
The normalization, Aint(E), is given by
Aint(E) = Fint(E)/2 (G (G (E))2) normalized cts arcmin-2 (19) (E))2) normalized cts arcmin-2 (19)
where the denominator is the renormalization factor such that the integral
of PSFint(E,r)2 r dr over the range r dr over the range 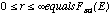 equals Fint(E). equals Fint(E).
Figure 2 compares the mirror
Gaussian width m with the
detector Gaussian width r with the
detector Gaussian width r versus angle
versus angle  . Figure 3 shows
the total Gaussian width G . Figure 3 shows
the total Gaussian width G ,
versus angle. From these figures we see that above ~ 14 arcminutes, the
mirror Gaussian term becomes dominant over the detector Gaussian term.
Figure 4 shows the change of shape of the components of the psf with
increasing off-axis angle, for 5 illustrative energies. ,
versus angle. From these figures we see that above ~ 14 arcminutes, the
mirror Gaussian term becomes dominant over the detector Gaussian term.
Figure 4 shows the change of shape of the components of the psf with
increasing off-axis angle, for 5 illustrative energies.
2.4 Test Results
The data shown here are a representative subset of the data used for
testing the off-axis psf algorithm. Radial profiles were extracted
centered on the source. When comparing the model and data at large angles
(i.e. in the outer region of the PSPC) it was crucial to define the center
of weight of the counts (which lies between the peak and hole) such that
we could produce a radial average of these features in each bin. We used
the IRAF imcntr routine (proto.imcntr). Given the approximate coordinates
of the center of an object, imcntr will compute a more accurate center
using the algorithms described in the Kitt Peak publication "Stellar
Magnitudes from Digital Images" under the Mountain Photometry Code
section. Briefly, this algorithm computes the sum of all the rows and the
sum of all the columns in the extraction box. Because the centers are
computed independently for x and y, the result may be considered inferior
to a true two-dimensional centering algorithm, but in practice the results
appear to be very usable.
The lowest 11 PI channels were rejected altogether to exclude problems
due to the variable lower limit discriminator for valid events due to the
variable instrument gain which is folded into these data. As described in
H92, we do not expect an acceptable fit to be obtained in the B band, due
to the "ghost imaging" effect. Additional sources falling within the
specified annuli were masked out of the analysis. No background
subtraction was carried out. Background rates were measured from the
events file and were later added to the predicted profile template for
each band. As in H92, a spectrum was also extracted for each source and
the predicted model could then be appropriately weighted with source
spectrum, for the energy band selected in each case. In addition, the
model was weighted with the amount of time the source spent at each
position on the detector, as the detector was wobbled across the sky
during the observations.
3 Results
These predicted psf templates are overlaid on some sample datasets in
Figure 5. We stress that the normalization of the model psf in each case
was also calculated using the equations presented here, thus NO FITTING
was performed. The normalization of the predicted psf was calculated such
that the integral under the predicted template is equal to the integral
under the observed psf.
It can be seen that even at this high signal-to-noise ratio, the psf
model provides an acceptable parameterization of the source profile for
all but the B-band (as expected). This model can be used to search for
extended emission (the limits of accuracy are evident by comparison with
the plots in Figure 5) and to determine the extraction cell required for
spectral and timing analysis.
Conclusions
An acceptable model for the off-axis dependence of the ROSAT PSPC psf has
been produced which can be used to estimate the correct extraction radii
required for data analysis of off-axis sources. In addition, this can be
used to determine whether off-axis sources are significantly extended. The
plots provided illustrate the limits of the accuracy of this
parameterization (particularly important for determination of significant
extent) and PIs are invited to contact the GOF team if they wish to
discuss any aspects of this parameterization. The comparison between model
and data is most difficult for sources observed in the outer region of the
PSPC detector, where radial profiles must be carefully centered to obtain
meaningful results.
The contact person at GSFC is Jane Turner (turner@lheavx.gsfc.nasa.gov or
LHEAVX::TURNER).
Acknowledgments
We thank Dave Davis for his help in the original extraction of some of the
off-axis data.
References
Hasinger, G., Turner, T.J., George, I.M. & Boese, G., 1992. Legacy, 2, 77 (CAL/ROS/92-001).
Hasinger, G., Turner, T.J., George, I.M. & Boese, G., 1993. Legacy, 3, 46
(CAL/ROS/92-001a).
Figures 1a-b
a) The in-flight psf for a point source located 40' off-axis. The center
of the detector is towards the upper left of the figure.
b) The PANTER psf for a point source located 40' off-axis. The center of
the detector is towards the upper left of the figure.
Figure 2 The widths of the
mirror (m[[sigma]]) and detector (r[[sigma]]) components to the Gaussian
term. This illustrates how the mirror effect begins to dominate outside of
~ 14 arcminutes. The lines of constant detector component represent (from
top to bottom) 0.28, 0.50, 2.0 and 1.0 keV. (The detector Gaussian has a
minimum between 1 and 2 keV, as detailed in Hasinger et al. 1992, thus the
inversion.)
Figure 3
The width of the mirror + detector Gaussian term versus off-axis angle.
The lines represent (from top to bottom) 0.28, 0.50, 2.0 and 1.0 keV. (The
detector Gaussian has a minimum between 1 and 2 keV, as detailed in
Hasinger et
al. 1992, thus the inversion.)
Figures 4a-e
a) The components of the PSPC psf versus off-axis angle at 0.188 keV.
b) The components of the PSPC psf versus off-axis angle at 0.284 keV.
c) The components of the PSPC psf versus off-axis angle at 0.5 keV.
d) The components of the PSPC psf versus off-axis angle at 1.0 keV.
e) The components of the PSPC psf versus off-axis angle at 1.7 keV.
Figures 5a-e
 Proceed to the next article
Proceed to the next article
 Return to the previous article
Return to the previous article
 Select another article
Select another article
HEASARC Home |
Observatories |
Archive |
Calibration |
Software |
Tools |
Students/Teachers/Public
Last modified: Monday, 19-Jun-2006 11:40:52 EDT
|